Pattern Formation in the Kuramoto Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
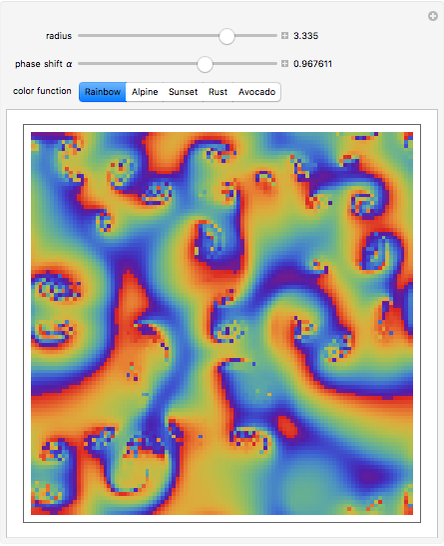
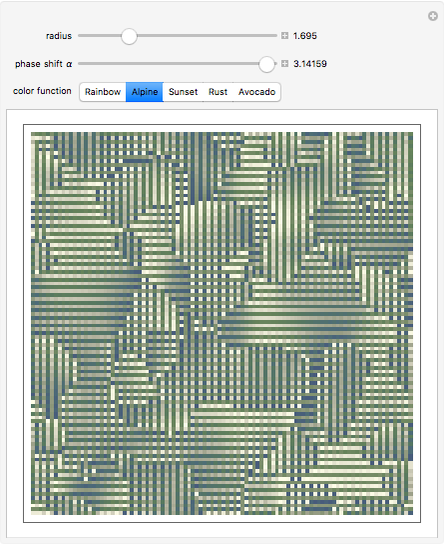
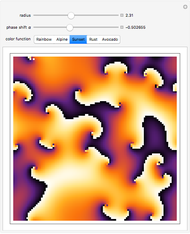
This Demonstration shows some decorative patterns that can arise in a two-dimensional Kuramoto model of coupled oscillators with a variable phase shift. The oscillators are coupled to their nearest neighbors within an adjustable radius on a grid with periodic boundary conditions. The image shown is determined by the phase shift of the oscillators after evolution of the system, starting with random phases.
Contributed by: Oliver K. Ernst (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
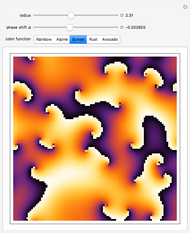
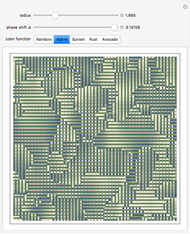
Snapshots 1 and 2: two examples of spiral patterns produced at phase shifts 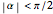
Snapshot 3: patterns that resemble plane waves at phase shift 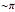
The Kuramoto model describes a set of oscillators coupled sinusoidally according to their phase differences.
In this Demonstration, a 100x100 grid of oscillators is initialized with random phases 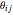 . Each oscillator is coupled to its nearest neighbors within a variable radius
. Each oscillator is coupled to its nearest neighbors within a variable radius 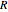 . The time evolution of the phases is governed by the differential equation
. The time evolution of the phases is governed by the differential equation
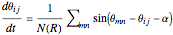 ,
,
with a phase shift  and the sum running over all oscillators at positions
and the sum running over all oscillators at positions  for which
for which  . The phases are updated according to the differential equation until interesting patterns are observed. The image displayed in the Demonstration shows the phases of each oscillator at the final timestep.
. The phases are updated according to the differential equation until interesting patterns are observed. The image displayed in the Demonstration shows the phases of each oscillator at the final timestep.
For further details, see the published work [1] on which this Demonstration is based. For general information on the Kuramoto model, see the Wikipedia article of the same name.
Reference
[1] P.-J. Kim, T.-W. Ko, H. Jeong, and H.-T. Moon, "Pattern Formation in a Two-Dimensional Array of Oscillators with Phase-Shifted Coupling," Physical Review E, 70(6), 2004.
Permanent Citation