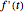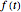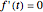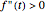Peak Retention Time Using Discrete Fourier Transform
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
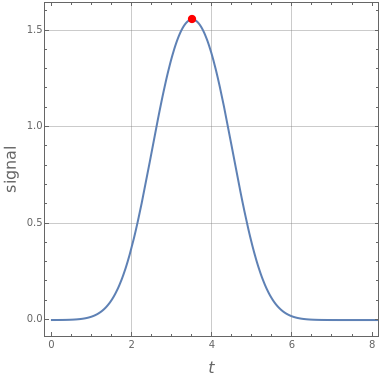
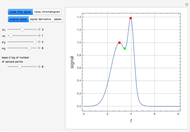
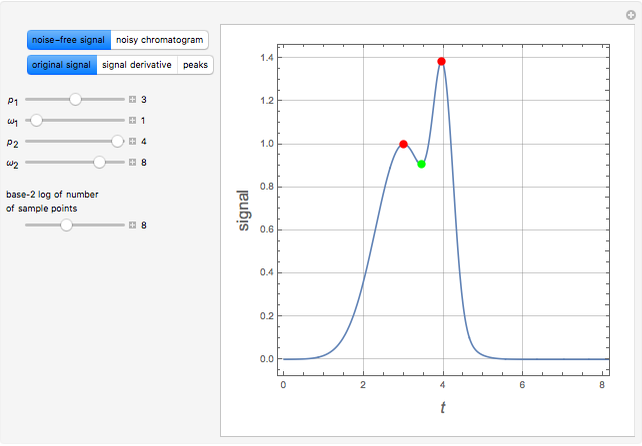
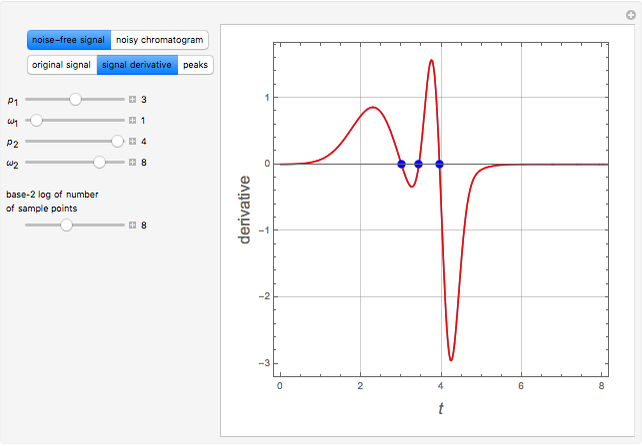
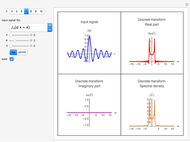
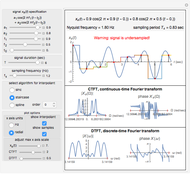
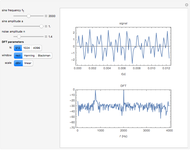
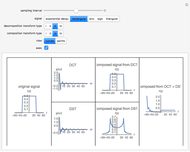
Consider a noise-free signal (e.g. a chromatogram of two chemical species), for instance, the sum of two Gaussian functions. This signal is given by 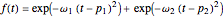 , where the user can set the values of parameters
, where the user can set the values of parameters  ,
,  ,
, 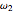 , and
, and 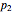 . These two Gaussian functions can show partial or even complete overlap.
. These two Gaussian functions can show partial or even complete overlap.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation