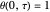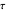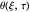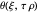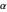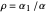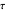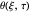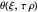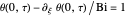Penetration of Potential in a Semi-Infinite Region
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
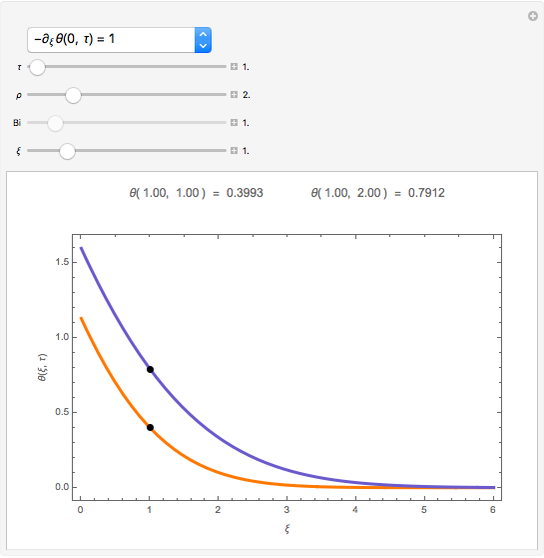
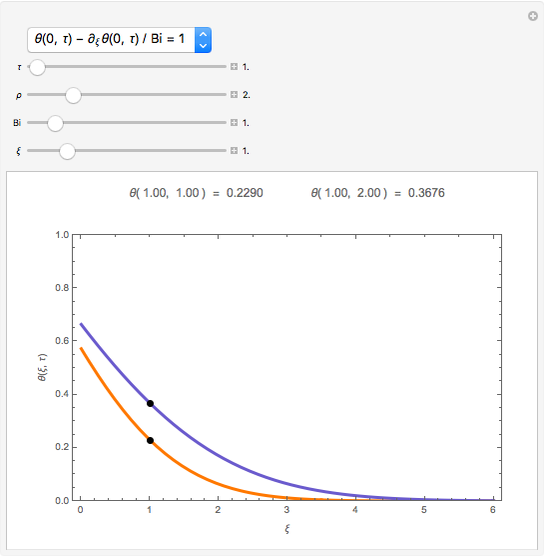
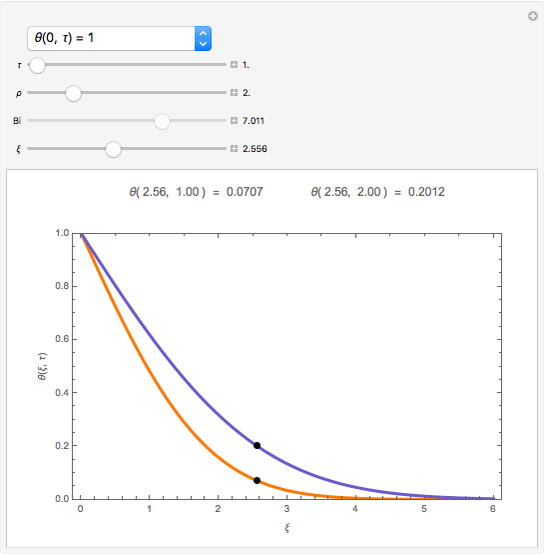
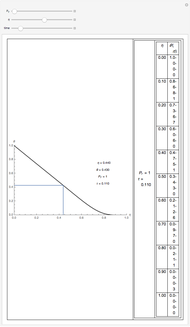
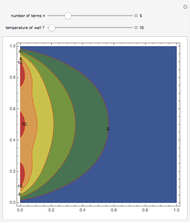
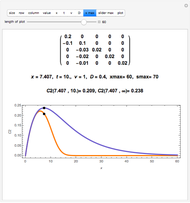
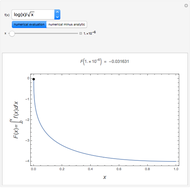
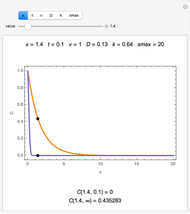
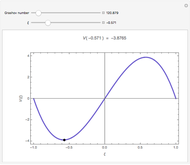
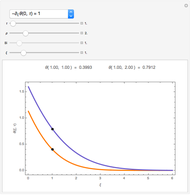
This Demonstration shows the penetration in a semi-infinite region of a dimensionless potential 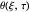 described by the model
described by the model 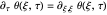 ,
, 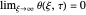 ,
,  with the three boundary conditions:
with the three boundary conditions: 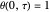 ,
, 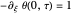 , and
, and 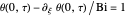 , where
, where  is dimensionless distance,
is dimensionless distance, 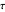 is dimensionless time, and Bi is the Biot number.
is dimensionless time, and Bi is the Biot number.
Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
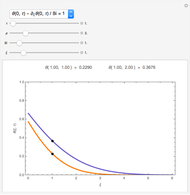
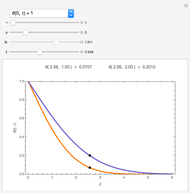
Snapshots
Details
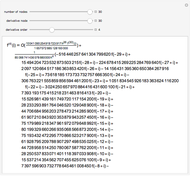
The problems
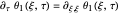 ,
, 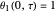 ,
, 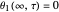 ,
, 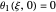 ,
,
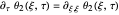 ,
, 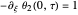 ,
,  ,
, 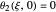 ,
,
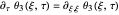 ,
, 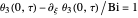 ,
,  ,
, 
have the following solutions:
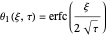 ,
,
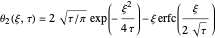 ,
,
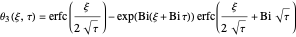 .
.
Permanent Citation