Details

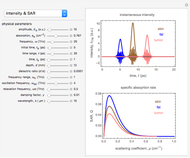
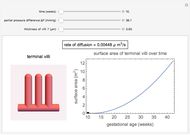
When tissue is penetrated, the dominant effects are scattering and absorption by polarizable molecules. The most important parameter in the interaction is the power density, 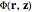(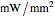). This is a function of power source delivered from a THz radiation source to the tissue, where input power is 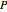(W), and the spot has a radius 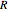(mm). The propagation of the scattered radiation is described by the photon transport equation

,

,

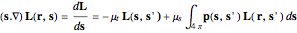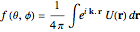where 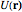is the potential energy. The amplitude 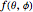depends on the potential, the scattering angle , and the target area . We can expand the plane waves in terms of Legendre polynomials to find an expression from the scattering amplitude and the differential cross section

.

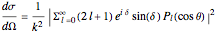The total cross section is 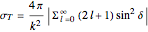. We verify directly that 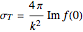, which is called the optical theorem.

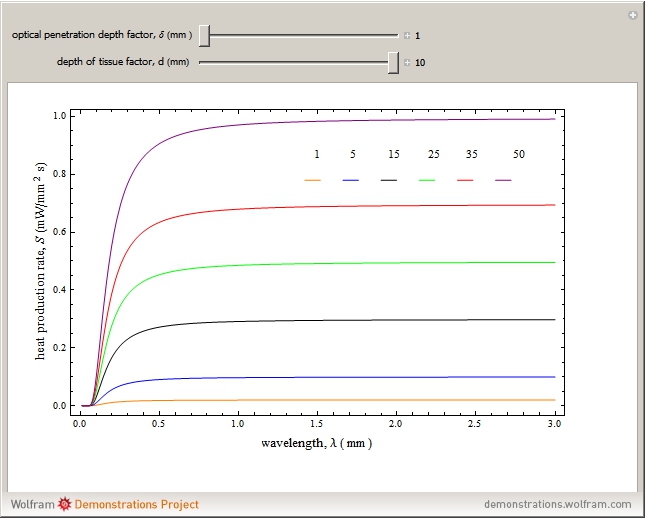
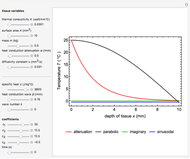
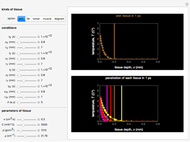
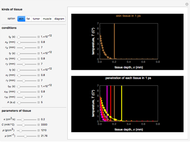
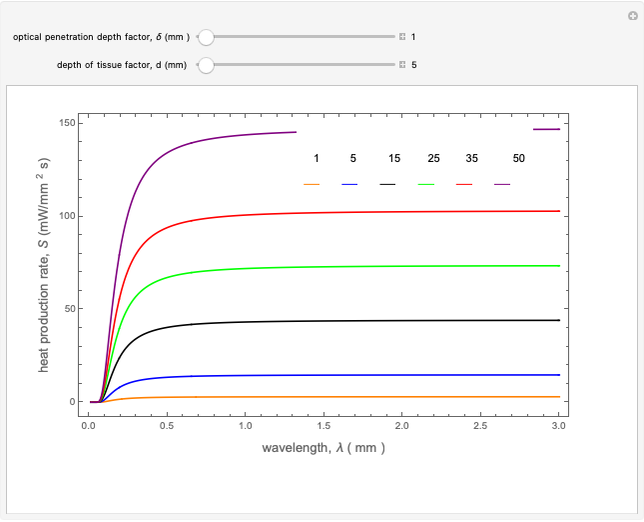
Snapshots 1, 2, and 3: The graphs show that the change from a shorter to a longer wavelength increases the heat production rate in a tumor cell volume slightly (measured in 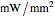). This means that shorter wavelengths contribute to the heat production more than the longer wavelengths. The longer wavelengths remain constant, with variation of tissue depth due to penetration of THz photon radiation , and also due to properties of tissue optical depth, . Other factors include the variation of the THz radiation power source 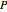and the variation of the wavelength 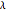, as well as the radiation photon incidence angle . Because the heat production is caused by the THz radiation beam propagating through the tissue with strong water absorption, the intensity is attenuated exponentially, due to the low scattering factor.

The following assumptions are made in this model: First, the frequency of the scattering radiation remains exactly the same as that of the incident radiation. Therefore, the scattering process is elastic. Second, any interaction between the scattered radiation particles themselves is neglected. Third, possible multiple scattering processes are likewise neglected. Fourth, the incident beam width is much larger than a typical range of the scattering potential, so that the particle will have a well-defined momentum.

References

[1] W. Hoppe, W. Lohmann, H. Markl, and H. Ziegler, Biophysics, New York: Springer-Verlag, 1983.

[2] G. Videen and D. Ngo, "Light Scattering from a Cell," in Optics of Biological Particles, NATO Science Series, Series II: Mathematics, Physics and Chemistry, Vol. 238, (A. Hoekstra, V. Maltsev, and G. Videen, eds.), New York: Springer, 2007.