Perfect 1-Factorizations of Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
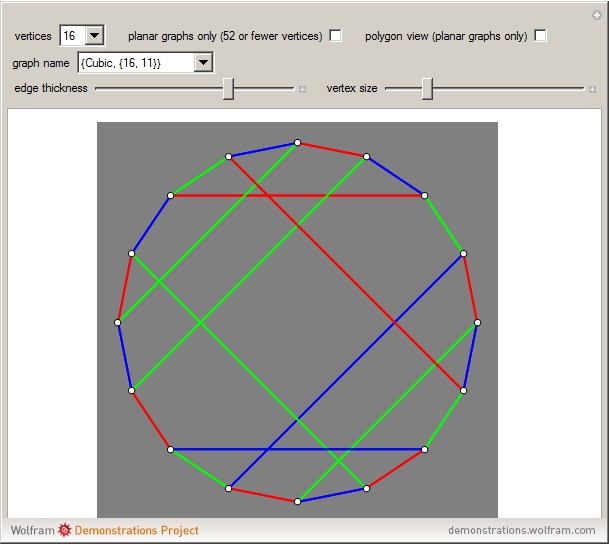
A perfect 1-factorization (P1F) of a  -regular graph is a proper edge coloring using
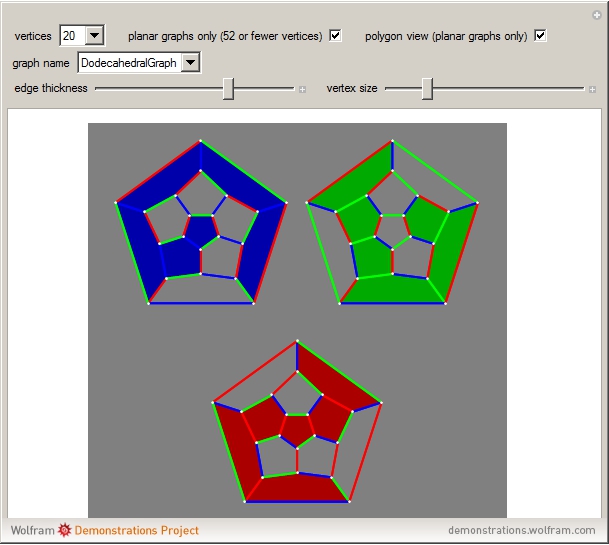
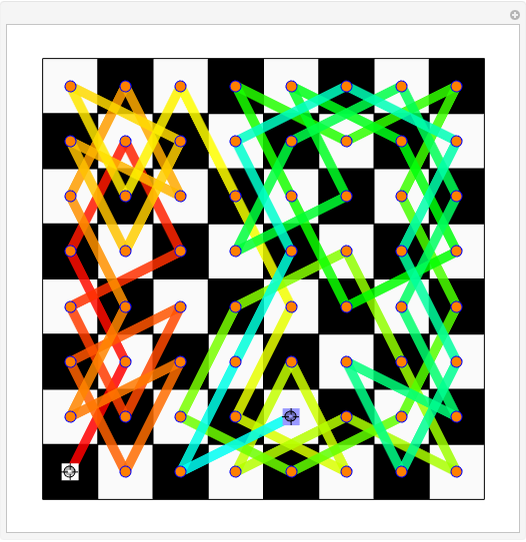
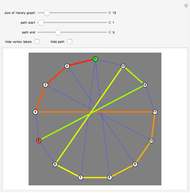
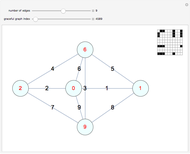
-regular graph is a proper edge coloring using  colors (meaning: two edges that meet at a vertex get different colors) so that the union of any two colors forms a Hamiltonian cycle. A graph with a P1F must have an even vertex count. This Demonstration shows P1Fs for over 1000 graphs in Mathematica's graph database, GraphData. When "polygon view" is chosen, each Hamiltonian cycle arising from a pair of colors is shown as a polygon.
colors (meaning: two edges that meet at a vertex get different colors) so that the union of any two colors forms a Hamiltonian cycle. A graph with a P1F must have an even vertex count. This Demonstration shows P1Fs for over 1000 graphs in Mathematica's graph database, GraphData. When "polygon view" is chosen, each Hamiltonian cycle arising from a pair of colors is shown as a polygon.
Contributed by: Stan Wagon (July 2012)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Perfect 1-factorizations are a difficult topic in graph theory, since they are not understood even for complete graphs. The outstanding conjecture is that every even complete graph admits a perfect 1-factorization; the first open case is 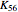 [1].
[1].
The P1Fs were found using a variety of techniques. The 3-regular case is simplest since one need only look for a Hamiltonian cycle such that the two matchings from the cycle together with the matching defined from the complement of the cycle form a P1F. One can search for random Hamiltonian cycles until a P1F is found.
For 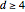 , one first develops a randomized algorithm for edge colorings, making use of random maximum matchings; that is fast thanks to the famous blossom algorithm. Often an edge coloring leads to a Hamiltonian decomposition (HD), which is a partition of all the edges of a graph into Hamiltonian cycles or, when
, one first develops a randomized algorithm for edge colorings, making use of random maximum matchings; that is fast thanks to the famous blossom algorithm. Often an edge coloring leads to a Hamiltonian decomposition (HD), which is a partition of all the edges of a graph into Hamiltonian cycles or, when  is odd, a set of Hamiltonian cycles plus one perfect matching. One can then search for a P1F by generating many random HDs and so obtaining a set of matchings by breaking each cycle of each HD apart into two matchings. The collection of matchings so obtained is then turned into a graph by connecting two matchings by an edge if they fit together to form a Hamiltonian cycle. This graph can then be searched for a complete subgraph of size
is odd, a set of Hamiltonian cycles plus one perfect matching. One can then search for a P1F by generating many random HDs and so obtaining a set of matchings by breaking each cycle of each HD apart into two matchings. The collection of matchings so obtained is then turned into a graph by connecting two matchings by an edge if they fit together to form a Hamiltonian cycle. This graph can then be searched for a complete subgraph of size  ; if such is found then the corresponding matchings form a P1F.
; if such is found then the corresponding matchings form a P1F.
References
[1] M. Li, J. Shu. "C-Codes: Cyclic Lowest-Density MDS Array Codes Constructed Using Starters for RAID 6." (Jul 18, 2012) arxiv.org/abs/1104.2547.
[2] J. H. Dinitz and D. R. Stinson, "Some New Perfect One-Factorizations from Starters in Finite Fields," Journal of Graph Theory, 13(4), 1989 pp. 405–415. www.emba.uvm.edu/~dinitz/preprints/perfect.from.starters.
[3] D. Bryant, B. M. Maenhaut, and I. M. Wanless, "A Family of Perfect Factorisations of Complete Bipartite Graphs," Journal of Combinatorial Theory A, 98(2), 2002 pp. 328–342. users.monash.edu.au/~iwanless/papers/perfactfamily.pdf.
Permanent Citation