Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

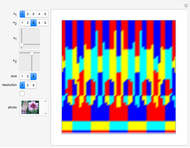
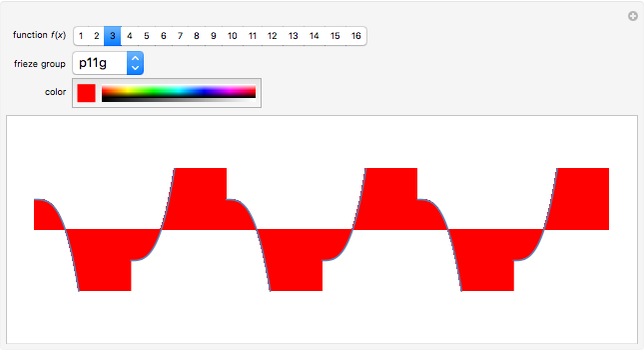
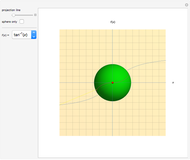
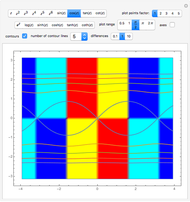
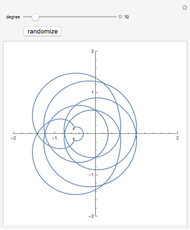
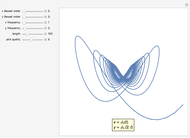
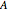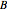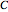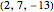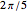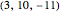Periodic Functions with m-Fold Symmetry of Type k

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Suppose that 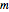and are relatively prime positive integers (i.e. ). Following [1, p. 14], define a curve with period 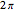to have 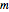-fold symmetry of type , of the form

[more]

.

This Demonstration shows graphs of the function , where , , and are complex coefficients and the frequencies , , and are integers. In particular, for the frequencies , the curve has fivefold symmetry of type 1. Increase the frequencies by 1 to get . The new curve has fivefold symmetry of type 2. Increase the frequencies by 1 once again. The curve has fivefold symmetry of type 3.

In the graphics, the green arrow shows the maximum modulus of the curve. Increasing the time from 0 to makes the green arrow skip two maxima and settle on a third. To get similar results for sevenfold symmetry, use the frequencies .

[less]

Contributed by: Izidor Hafner (March 2016)
Based on the work of: Frank A. Farris
Open content licensed under CC BY-NC-SA

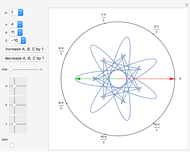
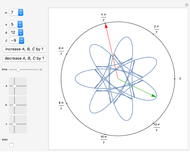
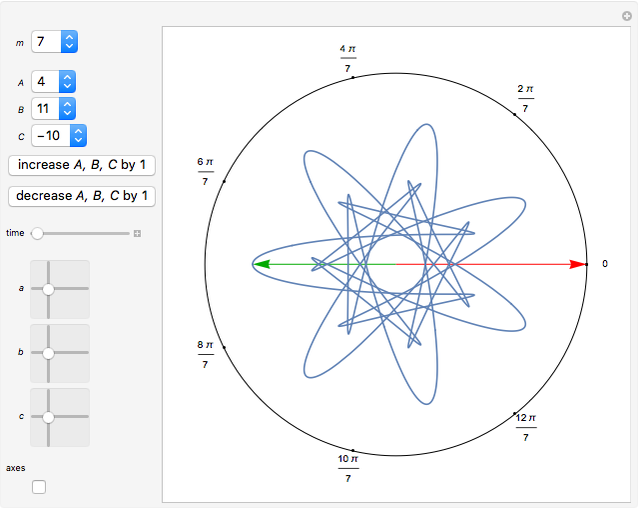
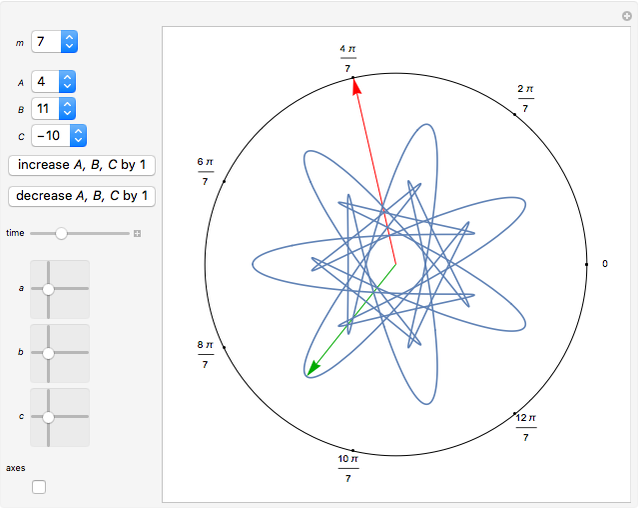
Snapshots

Details

The following theorem is shown in [1, pp. 13 ff.]:

Suppose that 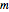and are integers and that all the frequency numbers 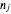in the finite sum

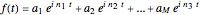
satisfy .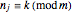

Then, for any choice of the coefficients 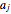, 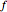satisfies the symmetry condition for all , so it has 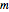-fold symmetry of type .

Reference

[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send