Permutations, Derangements, and Other Forbidden Position Problems Using Non-Attacking Rooks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
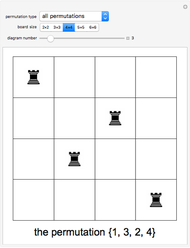
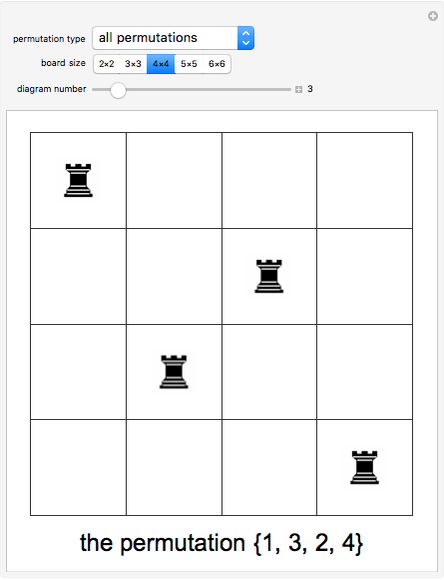
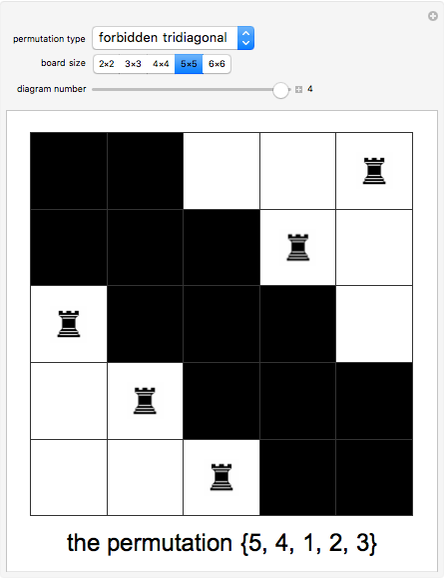
A permutation of  can be made to correspond to placing
can be made to correspond to placing  mutually non-attacking rooks on an
mutually non-attacking rooks on an  chessboard: if the permutation is
chessboard: if the permutation is  , place the
, place the  rook on the
rook on the  rank and
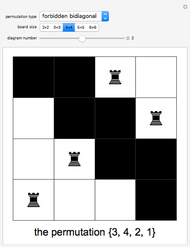
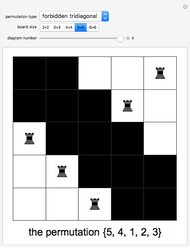
rank and  file. (Thinking of a chessboard as a matrix, rank and file mean row and column.) A derangement is a permutation where no element stays in its original position; it corresponds to placing the rooks on the board with the added requirement that the squares on the main diagonal are forbidden. Two other forbidden position problems are illustrated: avoiding the main diagonal and the diagonal just above it, and avoiding the main tridiagonal. In this Demonstration a chessboard consists of white squares, and black squares indicate forbidden positions.
file. (Thinking of a chessboard as a matrix, rank and file mean row and column.) A derangement is a permutation where no element stays in its original position; it corresponds to placing the rooks on the board with the added requirement that the squares on the main diagonal are forbidden. Two other forbidden position problems are illustrated: avoiding the main diagonal and the diagonal just above it, and avoiding the main tridiagonal. In this Demonstration a chessboard consists of white squares, and black squares indicate forbidden positions.
Contributed by: Marc Brodie (Wheeling Jesuit University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation