Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

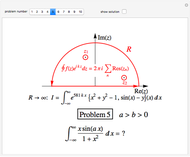
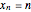Phenomenological Approximation to Newton's Cradle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

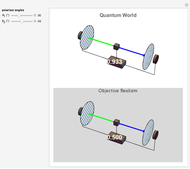
"Newton's cradle" (never actually mentioned by Newton himself) is an iconic executive desk toy consisting of five identical polished steel balls aligned with one another, each suspended from a frame a by pair of thin wires. When a ball at one end of the line is pulled back and released, it collides with the middle three balls, which remain stationary, while the ball at the other end of the line swings out to mirror the motion of the first ball. Then the motion reverses itself and repeats through a significant number of cycles. The canonical explanation of this phenomenon, commonly shown in many high school and college physics classes, is simply the conservation of momentum 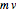and kinetic energy 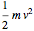in elastic collisions, these quantities being exchanged between the first and fifth balls through infinitesimal elastic deformations, similar to sound waves. Sometimes Newton's third law of action and reaction is evoked in the explanation.

[more]

So we have a neat experiment with a simple theoretical explanation, which satisfies the majority of physicists. However, several recent references, cited herein, note that, upon closer observation, the middle three balls do, in fact, oscillate very slightly. This can be attributed to the imperfect elasticity of the impacts, together with viscoelastic dissipation and possibly air resistance.

No consensus has yet been achieved for a rigorous solution of this problem. In fact, several videos of Newton's cradle displayed on the internet (YouTube) show small variations in the behavior of the swinging balls, depending evidently on small differences in construction and materials. In all cases, the preponderant tendency appears to be small-amplitude oscillations of the middle three balls, more or less in sync with the motion of the first and fifth balls.

In this Demonstration, we propose an empirical model containing a parameter , to estimate the fraction of kinetic energy transformed into elastic deformation in each collision along with the concomitant dissipation of energy. The canonical behavior is obtained in the limiting case, . The balls are assumed to be of unit diameter with their centers at equilibrium at , .

[less]

Contributed by: S. M. Blinder (June 2011)
After a Demonstration byEnrique Zeleny and detailed critiques by Giovanni Ciriani and Itai Saggev.
Open content licensed under CC BY-NC-SA

Snapshots

Details

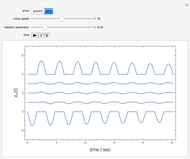
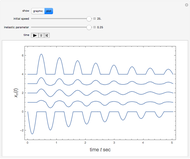
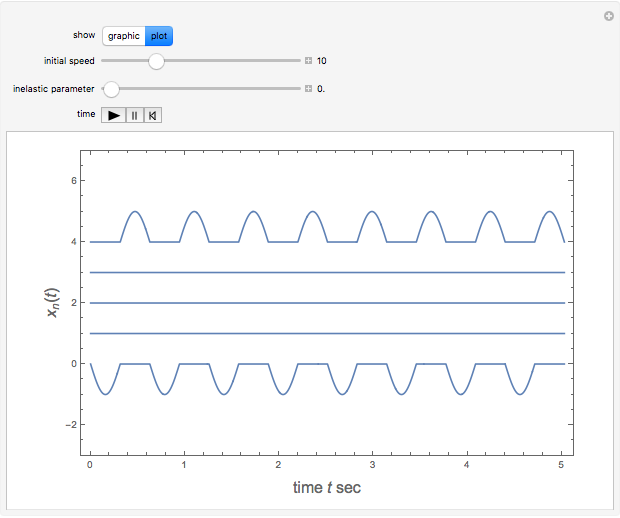
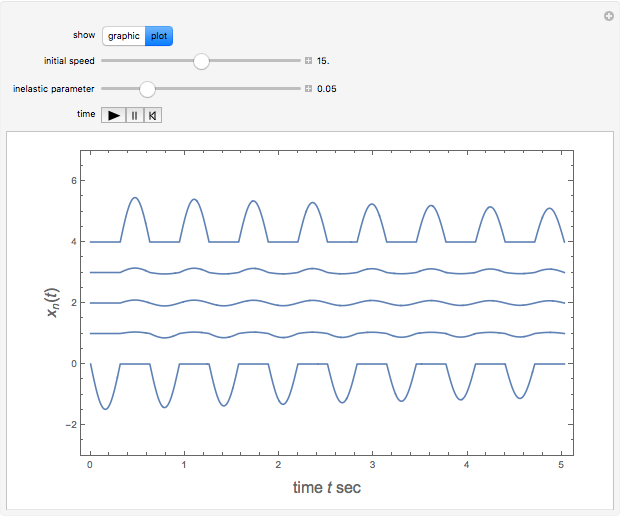
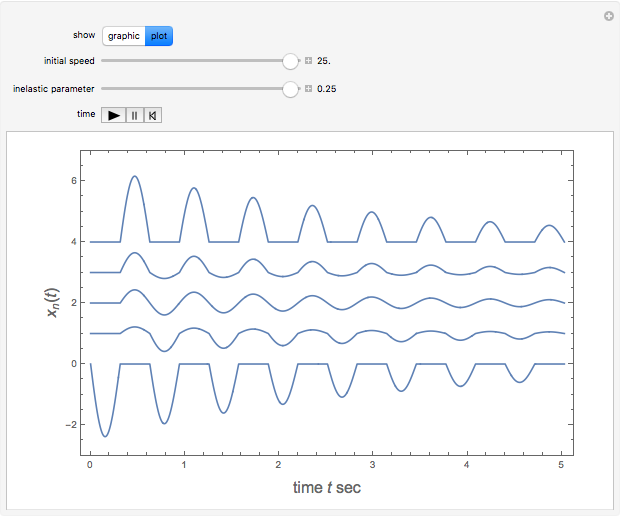
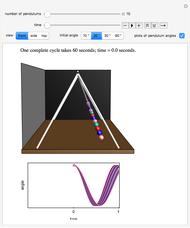
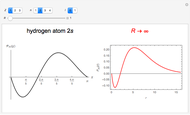
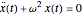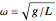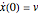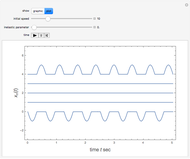
Left-hand ball behaves initially as a simple pendulum, well approximated by the linearized equation , with and initial condition , the speed at which the first ball hits the line of four others. The kinetic energy is partially converted into compression energy, which propagates the impulse along the chain. The function 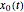approximates a modulated square wave, in which only negative values of 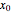appear. The fifth ball closely follows a complementary positive square-wave sinusoidal motion bounded by 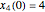. The approximate functional forms for the are plotted as functions of time. Snapshot 1 shows the canonical case with .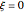

References

[1] S. Hutzler, G. Delaney, D. Weaire, and F. MacLeod, "Rocking Newton's Cradle," American Journal of Physics, 72(12), 2004 pp. 1508–1516.

[2] C. M. Donahue, C. M. Hrenya, A. P. Zelinskaya, and K. J. Nakagawa, "Newton's Cradle Undone: Experiments and Collision Models for the Normal Collision of Three Solid Spheres," Physics of Fluids, 20(11), 2008, 113301.

[3] C. F. Gauld, "Newton's Cradle in Physics Education," Science & Education, 15(8), 2006 pp. 597–617.

[4] E. J. Hinch and S. Saint–Jean, "The Fragmentation of a Line of Balls by an Impact," in Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 455(1989), 1999 pp. 3201–3220.

[5] V. Ceanga and Y. Hurmuzlu, "A New Look to an Old Problem: Newton’s Cradle," Journal of Applied Mechanics, 68(4), 2001 pp. 575–583.

[6] F. Hermann and M. Seitz, "How Does the Ball and Chain Work?" American Journal of Physics, 50(11), 1981 pp. 977–981.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send