Photon Number Distributions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
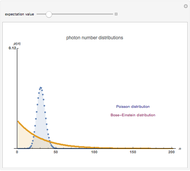
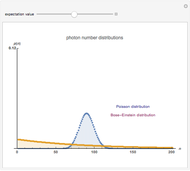
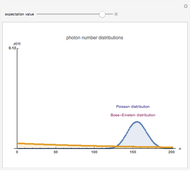
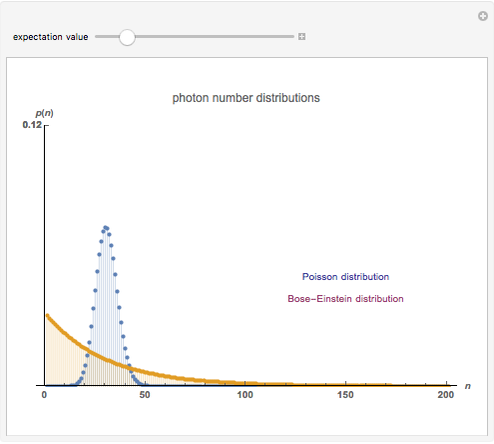
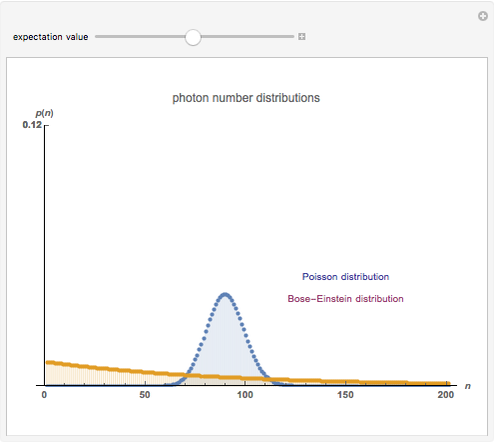
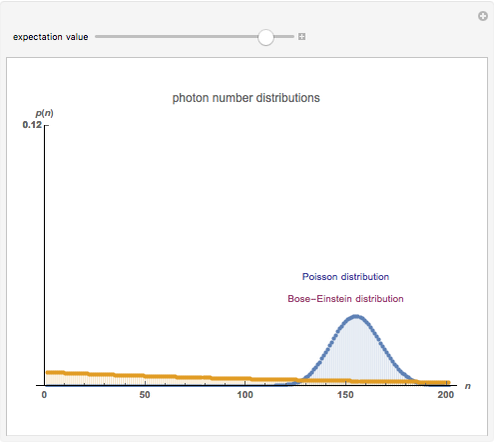
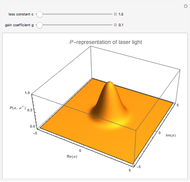
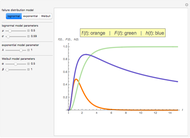
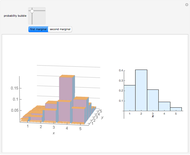
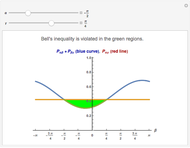
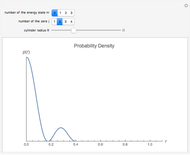
This Demonstration shows photon count distributions (probability distributions) of an ideal laser light source (Poisson distribution) and a thermal radiation source (Bose-Einstein distribution). In the interactive plots both functions have the same expectation value (mean). For the Poisson distribution, the expectation value and variance of the photon number  coincide; on the other hand, the variance of the thermal photon number distribution goes beyond its expectation value.
coincide; on the other hand, the variance of the thermal photon number distribution goes beyond its expectation value.
Contributed by: Reinhard Tiebel (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
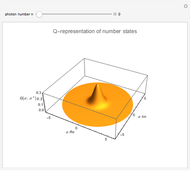
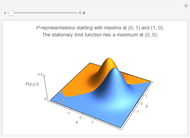
The probability of exactly measuring  photons in an optical radiation field depends on the characteristics of the light source. The radiation of an ideal single-mode laser shows a Poisson count distribution. In this case, the electromagnetic field can be described by a coherent state: this is an eigenstate of the annihilation operator (a non-Hermitian operator) corresponding to the optical radiation mode. The probability of finding
photons in an optical radiation field depends on the characteristics of the light source. The radiation of an ideal single-mode laser shows a Poisson count distribution. In this case, the electromagnetic field can be described by a coherent state: this is an eigenstate of the annihilation operator (a non-Hermitian operator) corresponding to the optical radiation mode. The probability of finding  photons is given by the square of the absolute value of the scalar product of the number state (i.e., the eigenstate of the photon number operator) and the coherent state. In contrast to this, the radiation of a thermal light source shows a Bose-Einstein count distribution. Coherent states produce an equals sign in the uncertainty relation for the momentum and position operators.
photons is given by the square of the absolute value of the scalar product of the number state (i.e., the eigenstate of the photon number operator) and the coherent state. In contrast to this, the radiation of a thermal light source shows a Bose-Einstein count distribution. Coherent states produce an equals sign in the uncertainty relation for the momentum and position operators.
Permanent Citation