Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Placing Dominoes on a Checkerboard

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

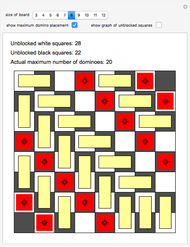
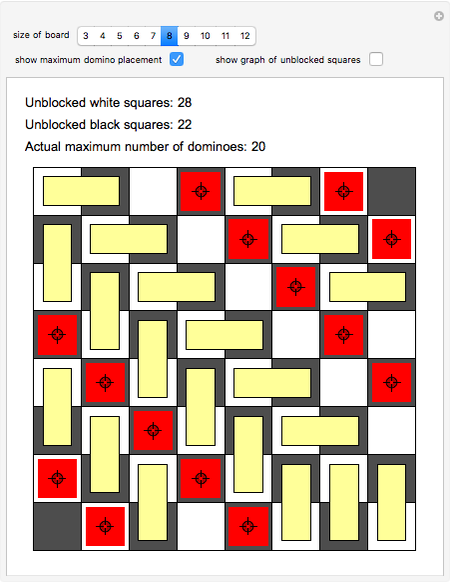
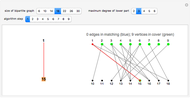
A classic puzzle asks for the placement of as many disjoint dominoes (1×2 tiles) as possible onto a checkerboard from which some squares have been removed. The problem can be solved by setting up a bipartite graph where one part consists of the white unblocked squares, the other consists of the black unblocked squares, and edges correspond to adjacency of squares. Then a maximum matching (a collection of disjoint edges that is as large as possible) in this graph leads to a solution of the domino problem. In this Demonstration, the blocked squares are red, the graph is shown in blue, and the maximum domino array is shown in yellow.

[more]

To add or remove blocked squares, -click or -click a square.

[less]

Contributed by: Stan Wagon (Macalester College) (July 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: an example in the 8×8 case where both white and black squares remain uncovered by dominoes

Snapshot 2: a similar example, again with a large discrepancy between the maximum possible, 20, and the maximum that can be placed, 14

Snapshot 3: the underlying bipartite graph

The algorithmic solution is based on the existence of a very fast algorithm—usually called the Hungarian algorithm—to find a maximum matching in a bipartite graph. The following two books are good references.

[1] R. A. Brualdi, Introductory Combinatorics, 4th ed., Saddle River, NJ: Prentice Hall, 2004.

[2] W. J. Cook, W. H. Cunningham, W. R Pulleyblank, and A. Schrijver, Combinatorial Optimization, New York: Wiley, 1998.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send