Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Plots of the Fermi-Dirac Distribution

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

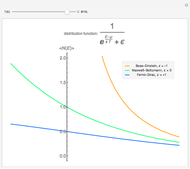
Fermi-Dirac statistics deals with identical and indistinguishable particles with half-integral spins. Electrons, protons, neutrons, and so on are particles (called fermions) that follow Fermi-Dirac statistics. Fermions obey the Pauli exclusion principle, which states that two fermions cannot occupy the same quantum state at the same time. The Fermi-Dirac distribution function gives the probability that a given energy level is occupied by a fermion for a system in thermal equilibrium.

[more]

The Fermi-Dirac distribution function of elements is given by , where is the Fermi energy of the element, is the Boltzmann constant, and is the probability that a quantum state with energy is occupied by an electron. This Demonstration shows the variation of the Fermi-Dirac distribution function of representative metals with energy at different temperatures.

[less]

Contributed by: Kallol Das (St. Aloysius College, Jabalpur, India) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

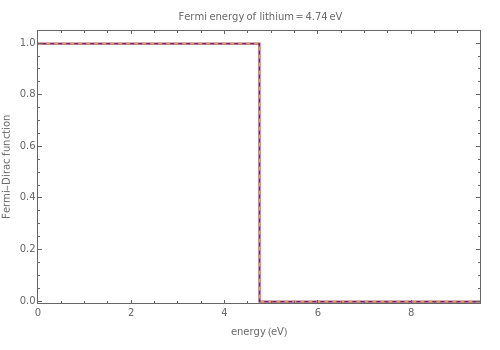
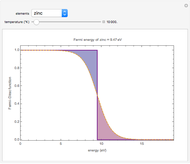
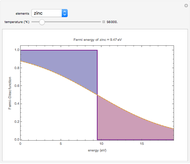
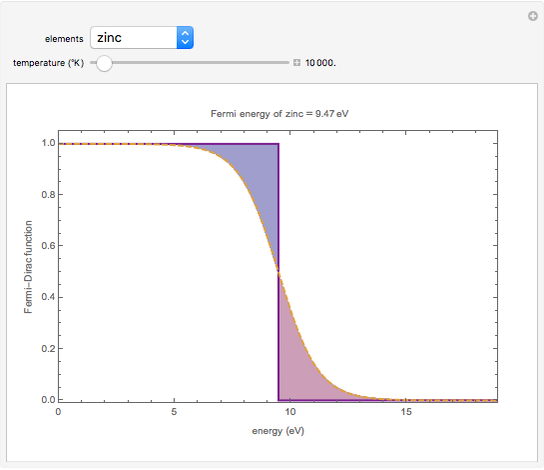
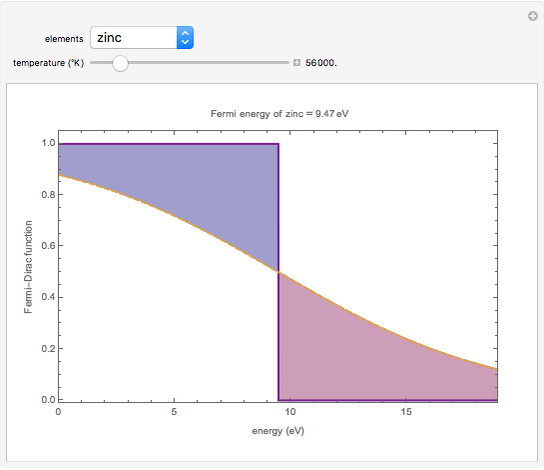
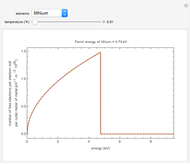
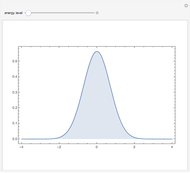
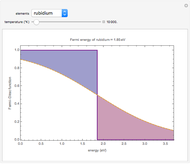
The dashed orange lines are plots of the Fermi-Dirac distribution function as a function of energy. At 0.0 °K, the highest occupied energy level is 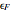.The blue section shows unoccupied energy levels at elevated temperatures, in the neighborhood of 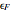.The red section shows occupied energy levels with energies greater than 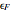at high temperatures. For comparison, the Fermi function at 0.001 °K is shown with bold purple lines.

The Fermi energy of elements is taken from N. W. Ashcroft and N. D. Mermin, Solid State Physics, New York: Holt, Rinehart and Winston, 1976.

The Fermi-Dirac distribution function details are taken from C. Kittel, Introduction to Solid State Physics, 5th ed., New York: Wiley, 1976.

Additional information on the free electron model can be found on Wikipedia.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send