Plotting Julia Sets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
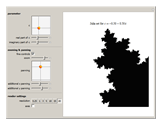
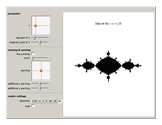
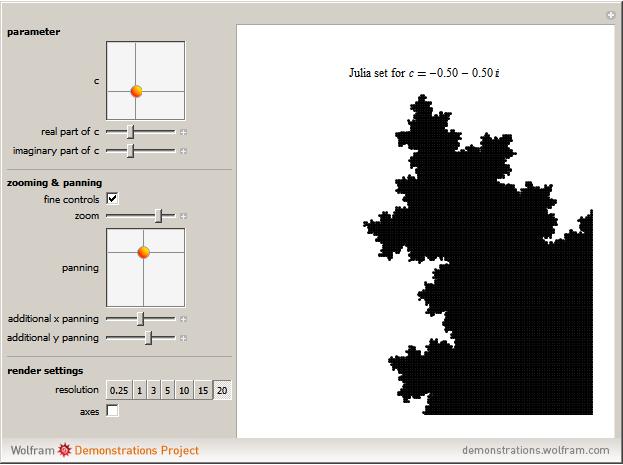
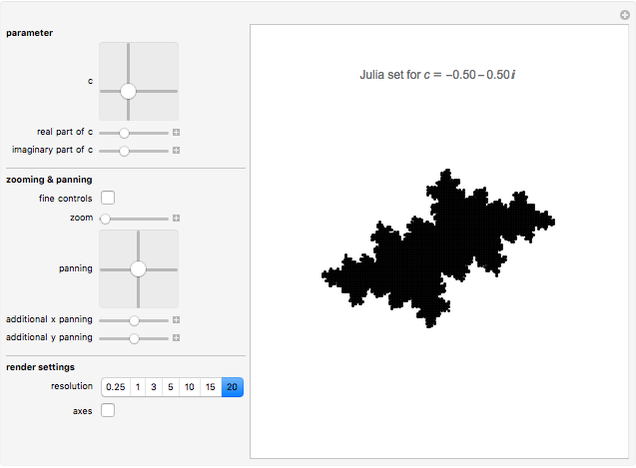
Change the  parameter for the quadratic Julia set using either the two-dimensional or one-dimensional sliders to explore endless variations of fractals. Explore the Julia set using the zoom and panning tools: dragging the "zoom" slider to the left zooms in, dragging to the right zooms out; pan in 2D using the "panning" two-dimensional slider or drag the "additional x panning" and "additional y panning" sliders for more precise control. As you zoom in and out, a very loose, rough low-resolution preview rendering of the fractal is displayed until you stop moving the slider and the display is given time to render fully. Once you have zoomed into a value less than 0.05, activate more precise zoom and panning controls by checking "fine controls". Now the "zoom" slider can zoom even closer, and the "additional x panning" and "additional y panning" sliders are more precise. Depending on how detailed a rendering you want, increase or decrease the resolution. Make the axes visible or invisible by checking the "axes" checkbox.
parameter for the quadratic Julia set using either the two-dimensional or one-dimensional sliders to explore endless variations of fractals. Explore the Julia set using the zoom and panning tools: dragging the "zoom" slider to the left zooms in, dragging to the right zooms out; pan in 2D using the "panning" two-dimensional slider or drag the "additional x panning" and "additional y panning" sliders for more precise control. As you zoom in and out, a very loose, rough low-resolution preview rendering of the fractal is displayed until you stop moving the slider and the display is given time to render fully. Once you have zoomed into a value less than 0.05, activate more precise zoom and panning controls by checking "fine controls". Now the "zoom" slider can zoom even closer, and the "additional x panning" and "additional y panning" sliders are more precise. Depending on how detailed a rendering you want, increase or decrease the resolution. Make the axes visible or invisible by checking the "axes" checkbox.
Contributed by: Owen Barrett (March 2011)
Open content licensed under CC BY-NC-SA
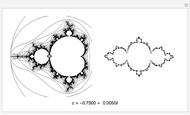
Snapshots
Details
Please be patient! Results may take several seconds to calculate.
To improve efficiency, the lattice of points iterated for a particular view is determined by the lower and upper  and
and  bounds and the zoom level. So at a zoom level of 0.0044 on an
bounds and the zoom level. So at a zoom level of 0.0044 on an  and
and  range of 0.008, 40401 points are generated at a density of
range of 0.008, 40401 points are generated at a density of 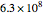 units squared. Each point is then iterated some
units squared. Each point is then iterated some  times proportional to the zoom level (the closer the zoom, the more iterations are required to render a detailed image; this is determined by a logarithmic function that preserves detail at very high zooms). In this way, no points are iterated that are not subsequently plotted.
times proportional to the zoom level (the closer the zoom, the more iterations are required to render a detailed image; this is determined by a logarithmic function that preserves detail at very high zooms). In this way, no points are iterated that are not subsequently plotted.
Not only is the rendering of the lattice optimized to waste no processing time, it is also cached so that recalling previously seen configurations is nearly instantaneous and requires no reiteration of the lattice, only a replotting. This caching mechanism also speeds up browsing within limited areas at the same zoom level because many of the lattice points generated have been cached, and so do not need to be reiterated.
You can increase or decrease the number of iterations by specifying a resolution under "render settings"; the number selected serves as a coefficient and does not specify the number of iterations outright.
The "fine controls" checkbox under "zooming & panning" is designed to be used at small scales. Since the fractals generated are infinitely detailed, this Demonstration is designed to accommodate extremely close zooms. In order to use the "fine controls" checkbox, browse to the desired area using the two-dimensional "panning" slider and the "zoom" slider. (In order to use the additional  and
and  sliders later, do not employ them now to navigate.) Once you have zoomed in such that the "zoom" slider reads a number equal to or smaller than 0.05, activate the "fine controls" checkbox. The maxima and minima of all one-dimensional "zooming & panning" sliders ("zoom", "additional x panning", and "additional y panning") will be redefined to make the sliders more precise. The two-dimensional slider, at this point, is too coarse to use, and so to navigate with the fine controls, use the "zoom" slider and the additional
sliders later, do not employ them now to navigate.) Once you have zoomed in such that the "zoom" slider reads a number equal to or smaller than 0.05, activate the "fine controls" checkbox. The maxima and minima of all one-dimensional "zooming & panning" sliders ("zoom", "additional x panning", and "additional y panning") will be redefined to make the sliders more precise. The two-dimensional slider, at this point, is too coarse to use, and so to navigate with the fine controls, use the "zoom" slider and the additional  and
and  panning sliders.
panning sliders.
Permanent Citation