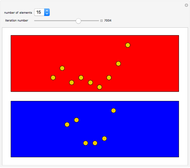
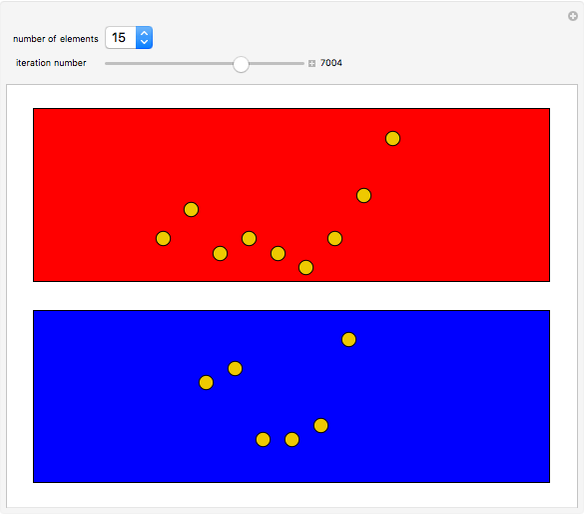
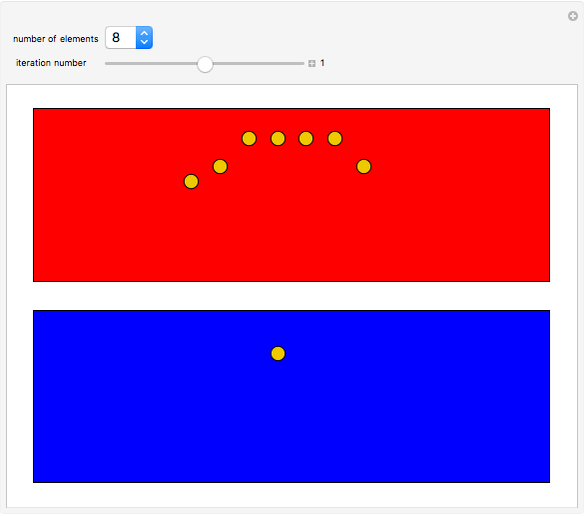
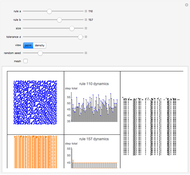
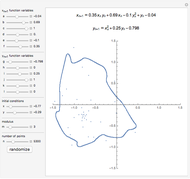
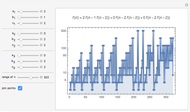
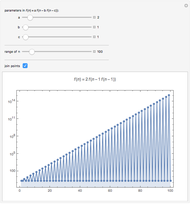
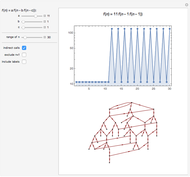
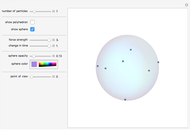
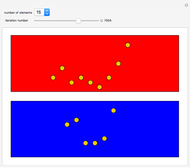
Roughly speaking, the Poincaré recurrence theorem states that, given infinite time, at some point an almost exact replica of a previous state of a system will be reached. This Demonstration has only two possible states in order to reduce computation time. You can cycle through the iterations to see the transition of elements (represented as disks) between the two states.