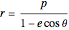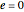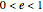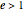Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Polar Plots of Conic Sections

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

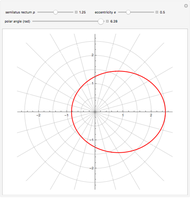
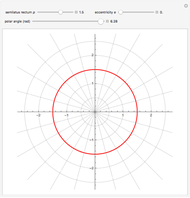
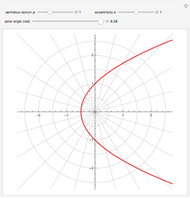
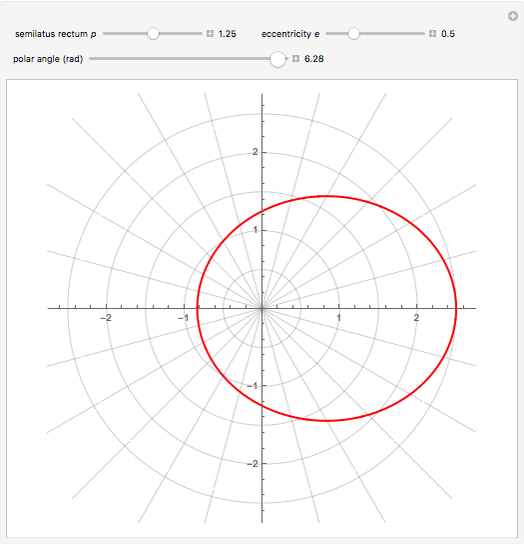
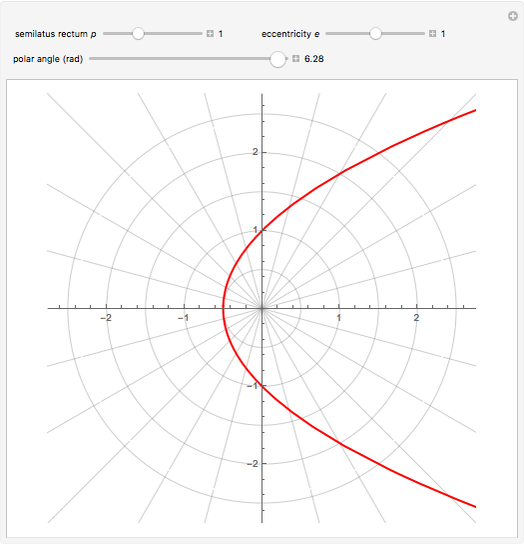
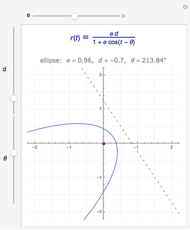
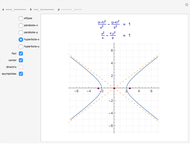
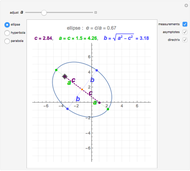
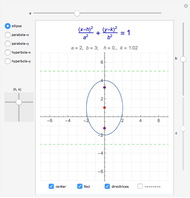
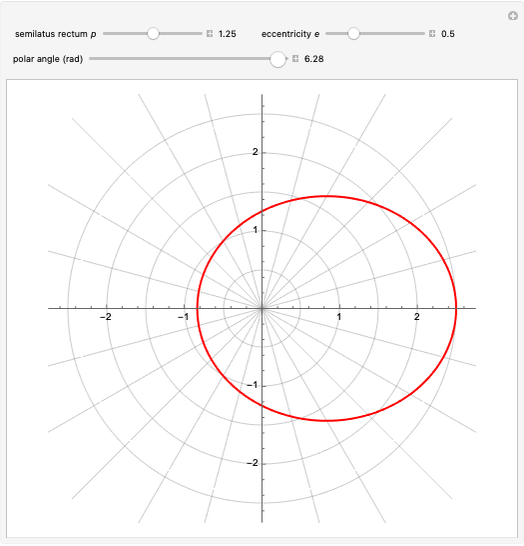
Conic sections (the circle, ellipse, parabola and hyperbola) can all be represented by an equation in polar coordinates:

[more]

,

where is the semilatus rectum and is the eccentricity of the curve. For the circle, ellipse, parabola and hyperbola, the eccentricity has the values , , and , respectively.

One focus of such a conic is at the origin. After selecting values of and , you can use the "polar angle" slider to trace out the polar curve by sweeping from 0 to . For , the plot generates both branches of a hyperbola.

[less]

Contributed by: S. M. Blinder (November 2019)
Open content licensed under CC BY-NC-SA

Details

A more general form for the polar equation is

,

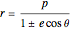where one focus is at the left-hand side of the conic for the minus sign (which we have used) but on the right-hand side of the conic for the plus sign. The alternative form

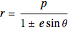
rotates the conics by 90°, with the semimajor axis oriented vertically.

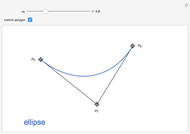
The following illustration shows the derivation of the formula for the case of a parabola (), with the focus at and the directrix (the vertical line) on the left.

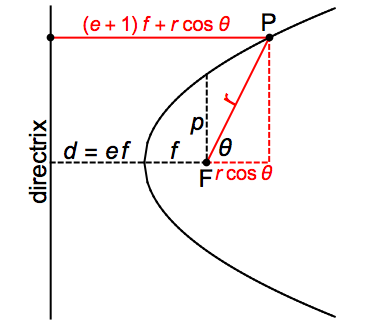
At every point 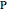on the curve, the defining relation is

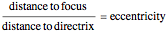or .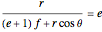

The semilatus rectum 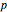is equal to when 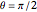. We obtain thereby

.

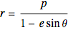Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send