PolyLog Function

Initializing live version

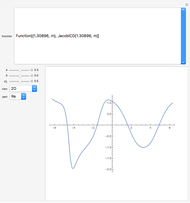
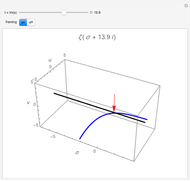
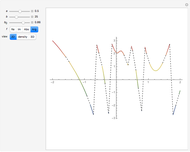
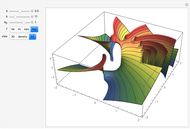
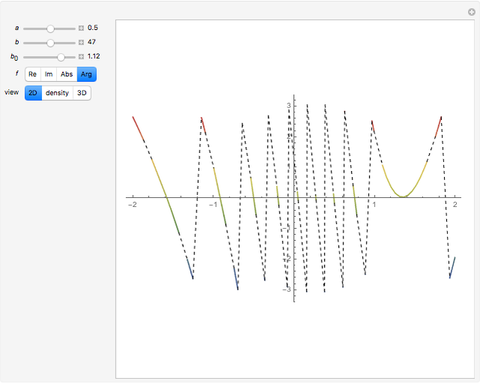
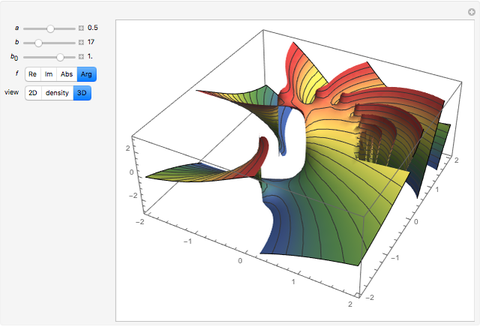
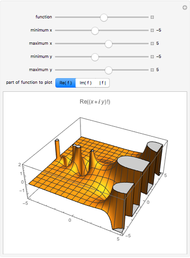
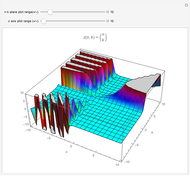
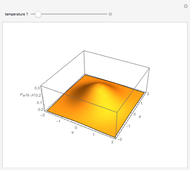
The polylogarithm function (or Jonquière's function) of index and argument is a special function, defined in the complex plane for and by analytic continuation otherwise. It can be plotted for complex values ; for example, along the celebrated critical line for Riemann's zeta function [1]. The polylogarithm function appears in the Fermi–Dirac and Bose–Einstein distributions and also in quantum electrodynamics calculations for Feynman diagrams. The 2D plot shows the function , and the 3D plot shows .

Contributed by: Enrique Zeleny (November 2014)
Open content licensed under CC BY-NC-SA

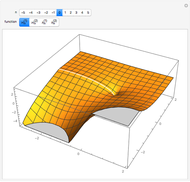
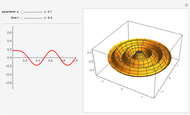
Snapshots

Details

The polylogarithm function is defined as

For , it is equivalent to the natural logarithm, . For and , it is called the dilogarithm and the trilogarithm; the integral of a polylogarithm is itself a polylogarithm

References

[1] L. Vepstas. "Polylogarithm, The Movie." (Nov 20, 2014) linas.org/art-gallery/polylog/polylog.html.

[2] T. M. Apostol. "Zeta and Related Functions." NIST Digital Library of Mathematical Functions, Version 1.0.9, Release date 2014-08-29. dlmf.nist.gov/25.12.

[3] Souichiro-Ikebe. "Polylogarithm Function." (Dec 4, 2015) Graphics Library of Special Functions (in Japanese). http://math-functions-1.watson.jp/sub1_spec_040.html.

Permanent Citation

Enrique Zeleny "PolyLog Function"
http://demonstrations.wolfram.com/PolyLogFunction/
Wolfram Demonstrations Project
Published: November 24 2014


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send

PolyLog Function

Snapshots

Details

Related Links

Permanent Citation