Poncelet's Porism for Quadrilaterals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
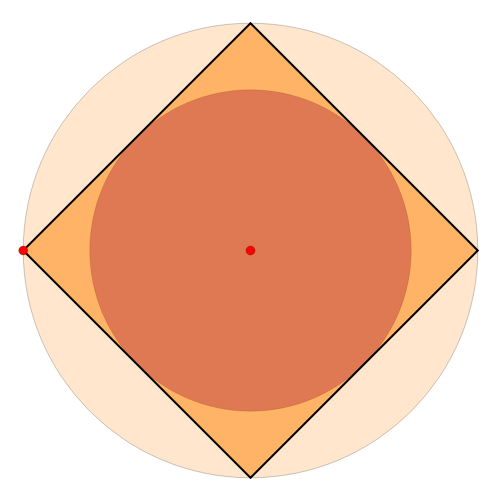
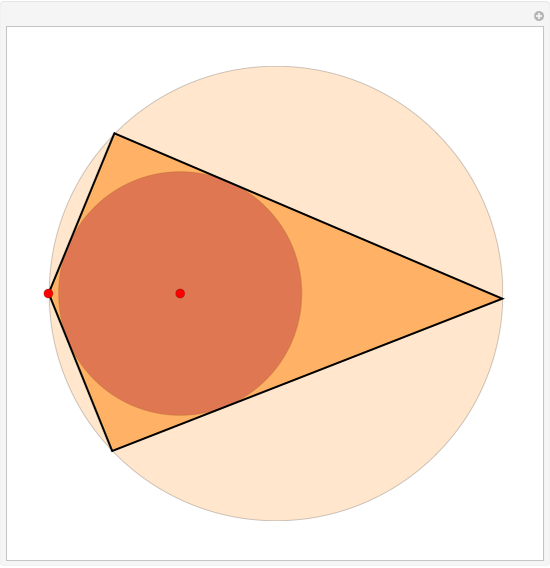
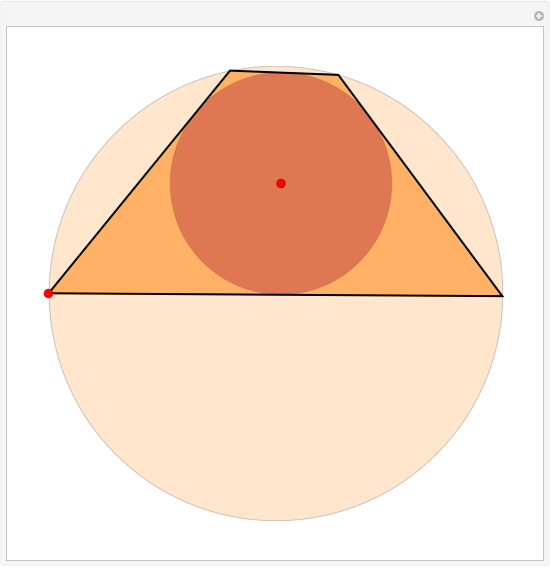
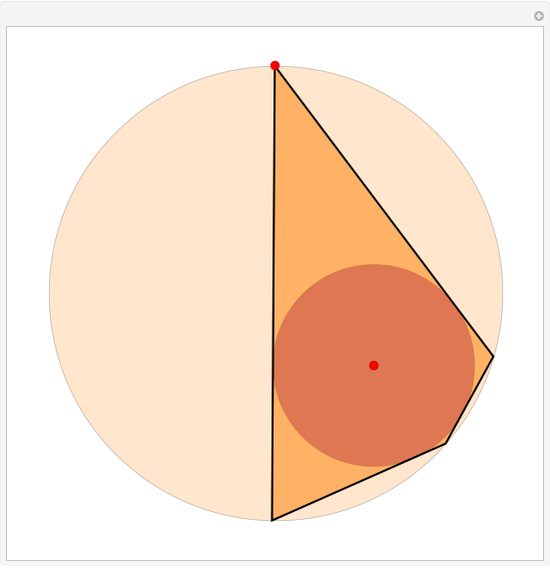
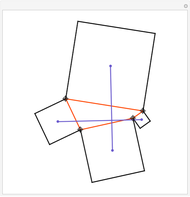
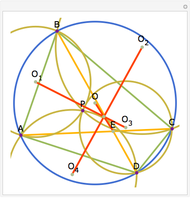
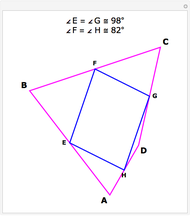
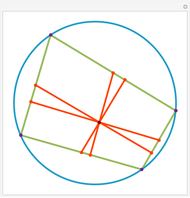
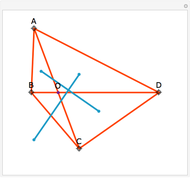
Assume circle  contains circle
contains circle  . If it is possible to inscribe a quadrilateral touching
. If it is possible to inscribe a quadrilateral touching  with its vertices and
with its vertices and  with its sides, then it is always possible to find a quadrilateral touching both circles and passing through any point of
with its sides, then it is always possible to find a quadrilateral touching both circles and passing through any point of  outside
outside  . Such quadrilaterals are called bicentric. For this Demonstration circle
. Such quadrilaterals are called bicentric. For this Demonstration circle  (in tan) is fixed and the position of circle
(in tan) is fixed and the position of circle  (in brown) can be changed by dragging the red center (the radius of
(in brown) can be changed by dragging the red center (the radius of  is obtained through Fuss's formula). You can change the position of the red vertex of the quadrilateral.
is obtained through Fuss's formula). You can change the position of the red vertex of the quadrilateral.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
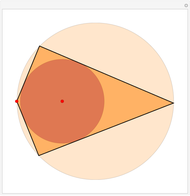
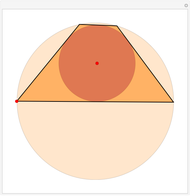
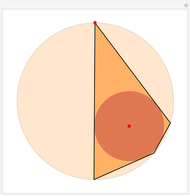
Snapshots
Details
detailSectionParagraphPermanent Citation
"Poncelet's Porism for Quadrilaterals"
http://demonstrations.wolfram.com/PonceletsPorismForQuadrilaterals/
Wolfram Demonstrations Project
Published: March 7 2011