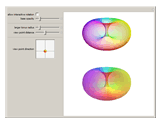
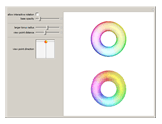
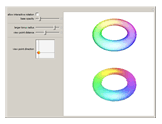
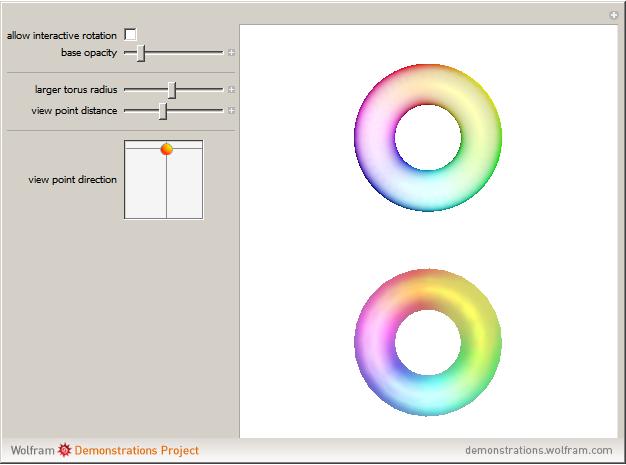
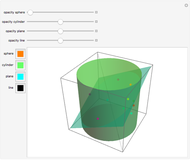
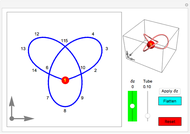
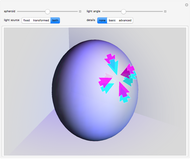
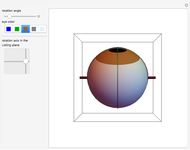
In Mathematica, opacity specified by Opacity[o] gives an opaque surface where the opacity is independent of the position. For curved surfaces this makes colors appear "flat". If the surface was made from a thin sheet of transparent material, the effective length of the optical path would depend on the angle between the surface normal and the view point. The optical path would be longest where the light rays would hit the surface parallel to its local tangent plane. The upper torus uses a position‐dependent opacity to model a larger absorption; the lower torus uses a constant opacity (equal to the average opacity of the upper image). The position‐dependent opacity results in darker edges and caustic‐like structures around cusp projections.