Primitive Pythagorean Triples 3: Ordered Tree Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
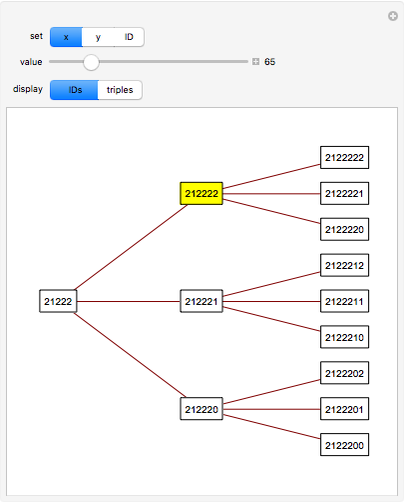
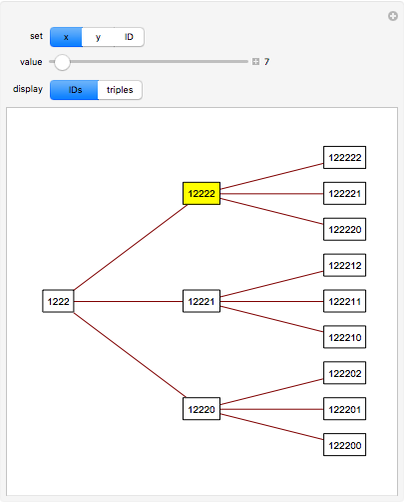
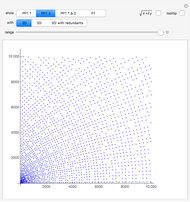
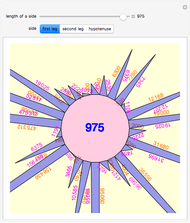
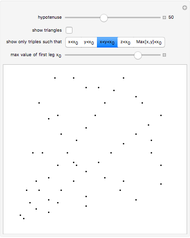
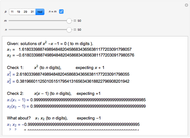
Primitive Pythagorean triples (PPTs) can be ordered, as shown here by assigning a unique integer to each instance. In practice, this allows a collection of PPTs to be generated and selected by a slider. Use the "set" control in conjunction with the "value" slider to jump to points in the ordering corresponding to a PPT with the first coordinate  , second coordinate
, second coordinate 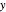 , or ID number in base 3 equal to the selected value in base 10.
, or ID number in base 3 equal to the selected value in base 10.
Contributed by: Robert L. Brown (March 2011)
Open content licensed under CC BY-NC-SA
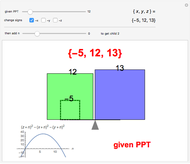
Snapshots
Details
Let 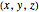 be a PPT, that is,
be a PPT, that is,  ,
, 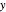 , and
, and  are positive integers such that
are positive integers such that 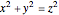 with
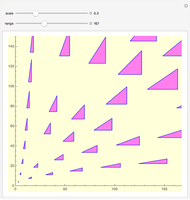
with 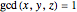 . A primitive right triangle has side lengths that form a PPT.
. A primitive right triangle has side lengths that form a PPT.
There are two ways to represent a particular PPT, by 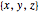 or
or 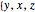 }. The corresponding primitive right triangles are inversely similar.
}. The corresponding primitive right triangles are inversely similar.
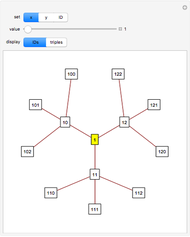
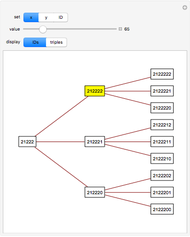
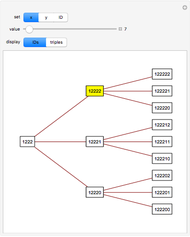
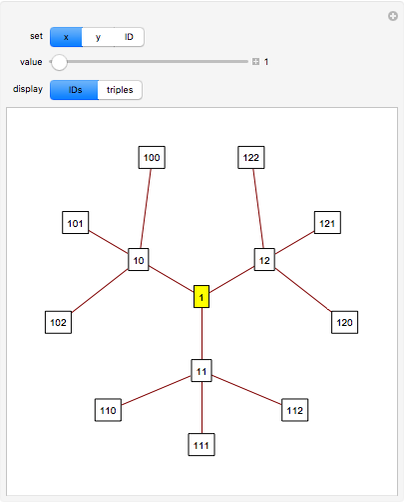
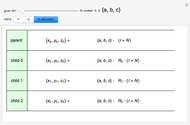
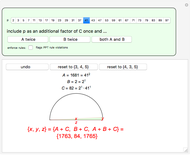
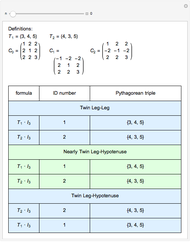
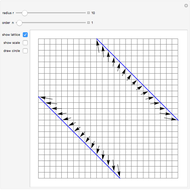
Each PPT can be represented by a unique base-3 number, called the PPT's ID number. The three children of a PPT have ID numbers formed by appending 0, 1, or 2 to the ID number of the PPT. The parent of a PPT has an ID number formed by dropping the last digit of the PPT's ID number.
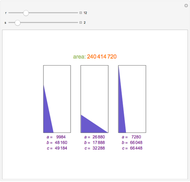
The Demonstration shows three levels of the PPT tree from a parent: the parent, three children, and nine grandchildren.
PPTs ordered in this manner form a pair of infinite ternary trees that are rooted (Wolfram MathWorld) and ordered (Wolfram MathWorld). The two roots are 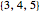 and
and 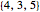 . The root of the tree to which any PPT belongs is identified by the first digit of its ID number. Only one tree is needed if inverse symmetry is ignored.
. The root of the tree to which any PPT belongs is identified by the first digit of its ID number. Only one tree is needed if inverse symmetry is ignored.
If 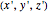 is a child of the PPT
is a child of the PPT 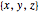 ,
, 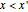 ,
, 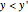 , and
, and  ', this can be used to prove completeness, that is, that all PPTs are in the tree.
', this can be used to prove completeness, that is, that all PPTs are in the tree.
The Demonstration "Primitive Pythagorean Triples 2: Ordered Pairs" proves uniqueness, that is, that the PPTs in the tree are all different.
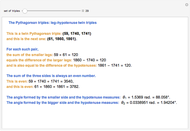
Suppose the ID number of a PPT is  . Then the ID number for the inversely similar PPT is found by switching 1 and 2 in
. Then the ID number for the inversely similar PPT is found by switching 1 and 2 in  . For example, {975, 448, 1073} and {448, 975, 1073} have ID numbers 11201 and 22102.
. For example, {975, 448, 1073} and {448, 975, 1073} have ID numbers 11201 and 22102.
Reference
[1] A. Hall, "Genealogy of Pythagorean Triads," Mathematical Gazette, LIV(390), 1970 pp. 377–379.
Permanent Citation