Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Prince Rupert's Cube

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

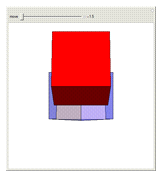
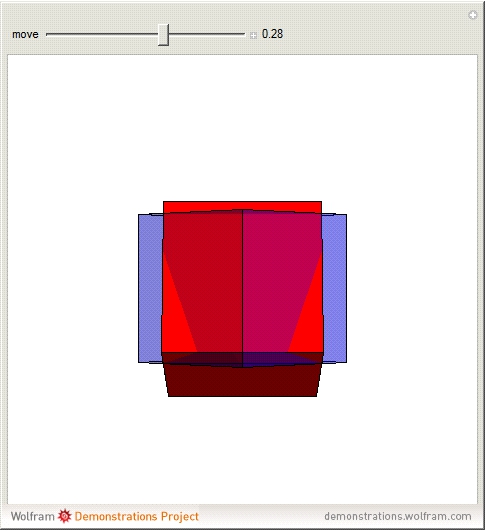
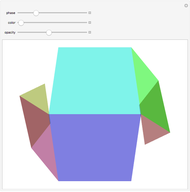
Prince Rupert's cube is the largest cube that can be made to pass through a given cube. The edge length of the red cube is times the length of the blue cube.

Contributed by: Izidor Hafner (January 2014)
Open content licensed under CC BY-NC-SA

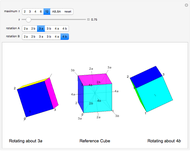
Snapshots

Details

References

[1] D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin Books, 1991 p. 195.

[2] Wikipedia. "Prince Rupert's Cube." (Nov 21, 2013) en.wikipedia.org/wiki/Prince_Rupert's_cube.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send