Problem 11340 of The American Mathematical Monthly
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
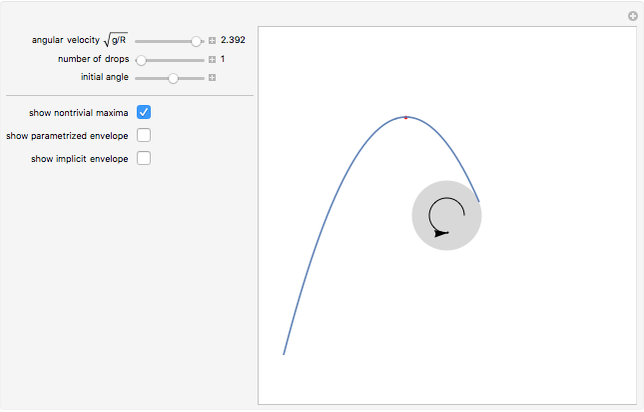
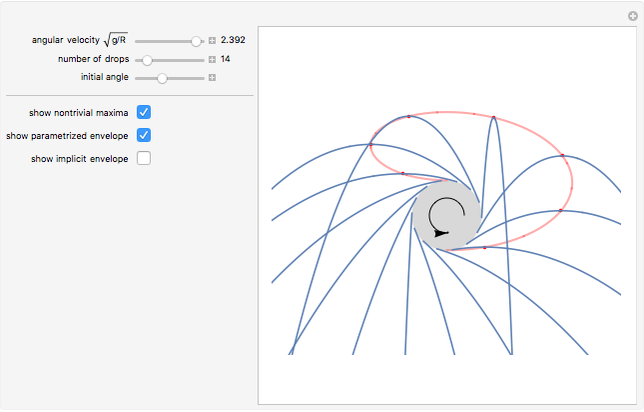
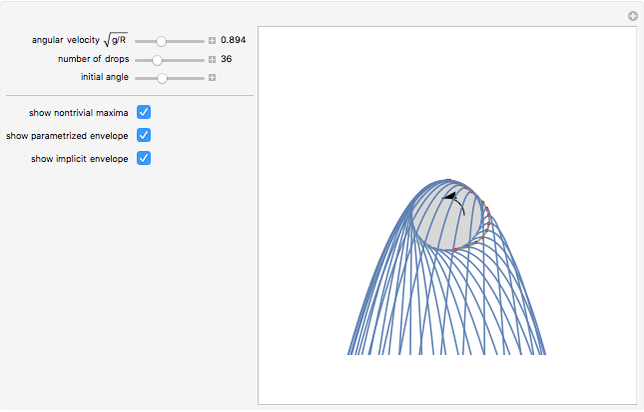
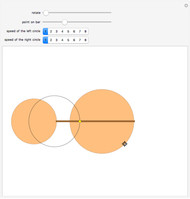
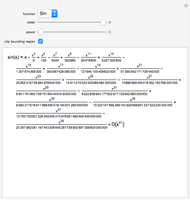
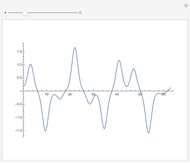
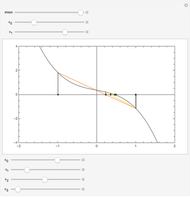
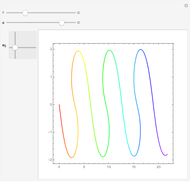
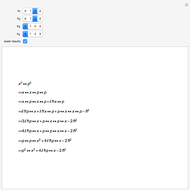
Problem 11340 of The American Mathematical Monthly (January 2008) asks for the following:
[more]
Contributed by: Michael Trott with permission of Springer. (March 2011)
From: The Mathematica GuideBook for Symbolics, second edition by Michael Trott (© Springer, 2008).
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information, see F. O. Goodman, "Mud Thrown from a Wheel Again", American Journal of Physics, 63(1), 1995 pp. 82–83.
Permanent Citation