Projection into Spaces Generated by Haar and Daubechies Scaling Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
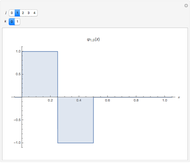
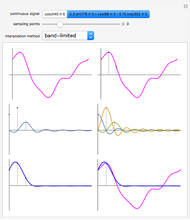
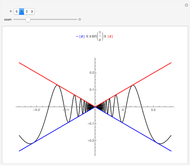
In this Demonstration,  selects which wavelet scaling function is used to project a function
selects which wavelet scaling function is used to project a function 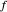 into a collection of subspaces
into a collection of subspaces 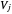 of
of 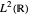 . The approximation space
. The approximation space  is defined as the span of
is defined as the span of  . Choices for
. Choices for  are the Haar scaling function and the Daubechies scaling function with two vanishing moments.
are the Haar scaling function and the Daubechies scaling function with two vanishing moments.
Contributed by: Sijia Liang and Bruce Atwood (February 2013)
(Beloit College)
Open content licensed under CC BY-NC-SA
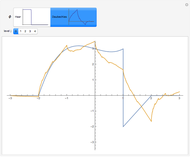
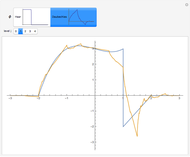
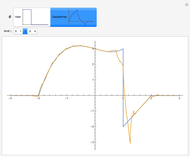
Snapshots
Details
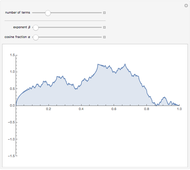
Both scaling functions generate orthonormal bases. Thus the projection of  into a
into a 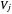 space is given by
space is given by  , where
, where  .
.
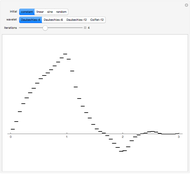
For students: The function  is nonzero on
is nonzero on 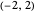 and the Haar scaling function is nonzero on
and the Haar scaling function is nonzero on 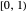 . From this, determine what values of
. From this, determine what values of  (as a function of
(as a function of 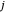 ) make
) make  nonzero. What about for the Daubechies scaling function that is nonzero on
nonzero. What about for the Daubechies scaling function that is nonzero on 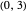
 ? You can check your answers by looking at the source code.
? You can check your answers by looking at the source code.
Scaling functions are the basic building blocks for multiresolution analysis in wavelet theory. For more information see [1]. This Demonstration is based on an example from that book.
Reference
[1] D. K. Ruch and P. J. Van Fleet, Wavelet Theory: An Elementary Approach with Applications, Hoboken, NJ: John Wiley & Sons, 2009.
Permanent Citation