Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

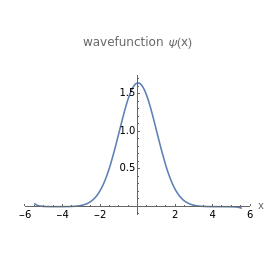
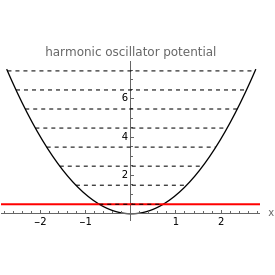
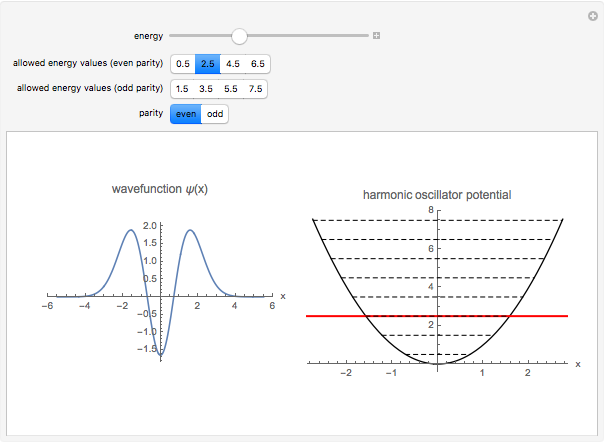
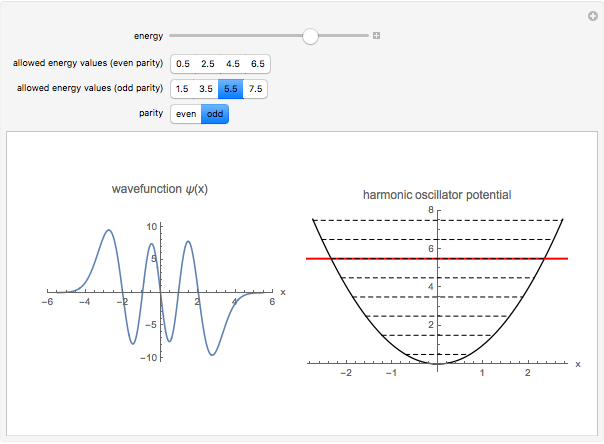
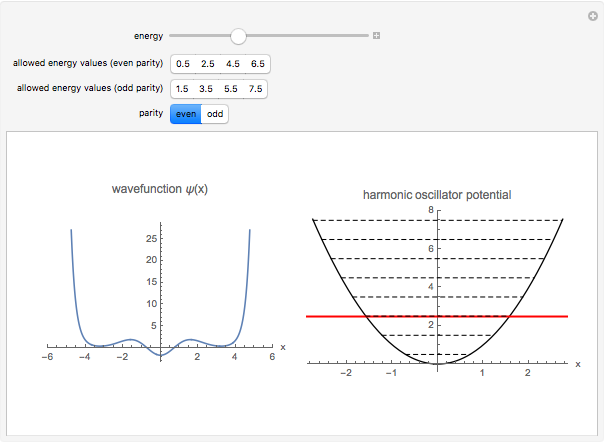
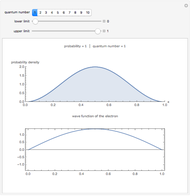
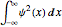Quantized Solutions of the 1D Schrödinger Equation for a Harmonic Oscillator

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

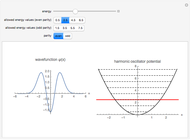
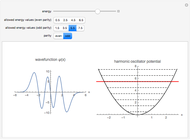
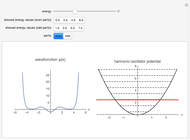
This illustrates the quantized solutions of the Schrödinger equation for the one-dimensional harmonic oscillator:

[more]

.

As you vary the energy, the normalization and boundary conditions (for even or odd parity) are only satisfied at discrete energy values of the solution of the second-order ordinary differential equation. Boundary conditions are met when as and normalization is possible when exists.

[less]

Contributed by: Jamie Williams (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send