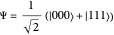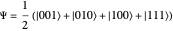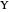Quantum Computer Simulation of GHZ Experiment

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
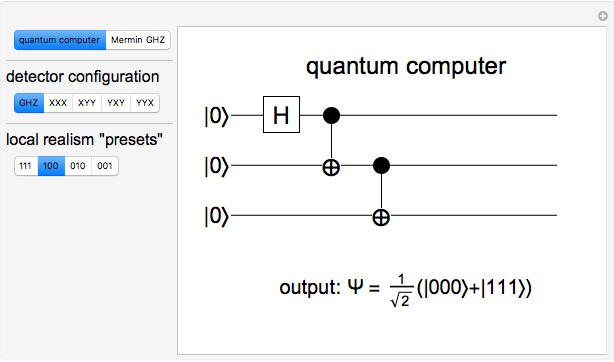
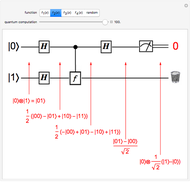
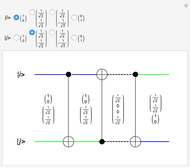
An entangled state of three photons in a superposition, either with all horizontally polarized (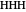 ) or with all vertically polarized (
) or with all vertically polarized (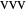 ), is known as a Greenberger–Horne–Zeilinger (GHZ) state [1, 2]. It is represented by the state vector
), is known as a Greenberger–Horne–Zeilinger (GHZ) state [1, 2]. It is represented by the state vector 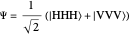 . A measurement on any one of the photons, using a two-channel polarizer, would give 50% probability for either
. A measurement on any one of the photons, using a two-channel polarizer, would give 50% probability for either 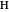 or
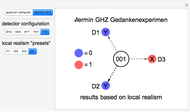
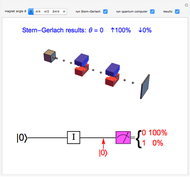
or 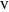 . Measurements on the other two photons would then be found to show the same polarization. In the canonical GHZ experiment, measurements are performed on the three entangled photons using two-channel polarizers
. Measurements on the other two photons would then be found to show the same polarization. In the canonical GHZ experiment, measurements are performed on the three entangled photons using two-channel polarizers 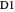 ,
, 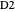 and
and 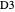 set to orientations different from the original
set to orientations different from the original 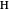 and
and 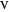 , which we denote by
, which we denote by 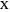 and
and 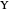 . The
. The 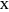 polarizations are at angles of
polarizations are at angles of 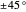 with respect to the original polarizations, such that
with respect to the original polarizations, such that 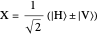 . The
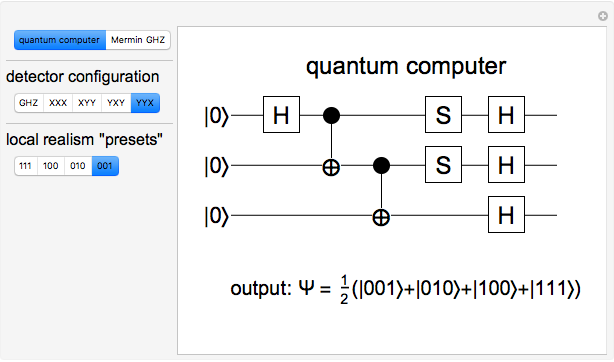
. The  polarizations are left and right circular polarizations, represented by
polarizations are left and right circular polarizations, represented by  . The polarization detectors are set in one of four possible combinations:
. The polarization detectors are set in one of four possible combinations:  ,
, 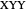 ,
,  or
or 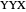 . We use binary notation, 0 and 1, to label the two possible polarizations for either the
. We use binary notation, 0 and 1, to label the two possible polarizations for either the 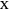 or
or  orientation. For the
orientation. For the 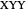 ,
, 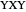 or
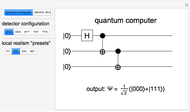
or 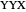 configuration, we observe four equally probable results, which we designate 001, 010, 001 and 111. For
configuration, we observe four equally probable results, which we designate 001, 010, 001 and 111. For 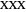 , we again observe four equally probable results, but now 000, 011, 101 or 110. In all of these cases, any two detector readings, say those of
, we again observe four equally probable results, but now 000, 011, 101 or 110. In all of these cases, any two detector readings, say those of  and
and 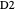 , unambiguously determine the reading of
, unambiguously determine the reading of  . For example, for configuration
. For example, for configuration 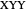 , if the first two detectors read 01 or 10, the third would then show 0.
, if the first two detectors read 01 or 10, the third would then show 0.
Contributed by: S. M. Blinder (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
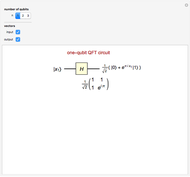
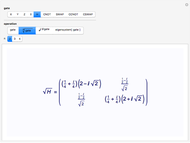
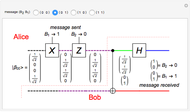
The Hadamard gate  (not to be confused with the horizontal polarization, also called
(not to be confused with the horizontal polarization, also called 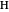 ) acts on a qubit in one of the basis states to produce a linear combination of the two basis states. Specifically
) acts on a qubit in one of the basis states to produce a linear combination of the two basis states. Specifically  and
and  . As a unitary operator,
. As a unitary operator, 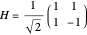 . The
. The 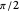 -phase shift gate
-phase shift gate 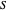 is represented by
is represented by  .
.
References
[1] D. M. Greenberger, M. A. Horne, A. Shimony and A. Zeilinger, "Bell's Theorem without Inequalities," American Journal of Physics, 58(12), 1990 pp. 1131–1143. doi:10.1119/1.16243.
[2] J.-W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter and A. Zeilinger, "Experimental Test of Quantum Nonlocality in Three-Photon Greenberger–Horne–Zeilinger Entanglement," Nature, 403, 2000 pp. 515–519. doi:10.1038/35000514.
[3] G. Fano and S. M. Blinder, Twenty-First Century Quantum Mechanics: Hilbert Space to Quantum Computers, New York: Springer, 2017.
[4] N. D. Mermin, "Quantum Mysteries Revisited," American Journal of Physics, 58(8), 1990 pp. 731–734. doi:10.1119/1.16503.
Permanent Citation