Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

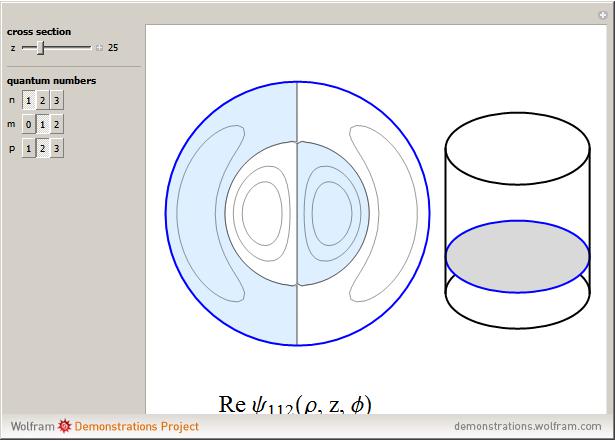
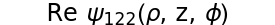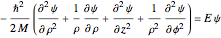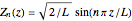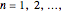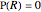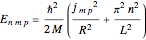Quantum-Mechanical Particle in a Cylinder

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

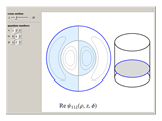
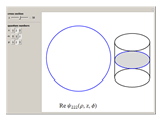
This is one of the three classic particle-in-a-box problems in elementary quantum mechanics, along with the cuboid and the sphere. For a particle of mass in a right circular cylinder of radius 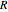and altitude , the Schrödinger equation in cylindrical coordinates , , can be written as

[more]

.

The equation is separable, as . The and factors are elementary functions: , with and , with . The equation for can be reduced to with the boundary condition . The solutions are Bessel functions such that is the zero of the Bessel function . The total energy is then given by .

This Demonstration shows contour plots of the wavefunction through horizontal cross sections of the cylinder, representing constant values of between 0 and . The wavefunction is positive in the light blue regions.

[less]

Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send