Quantum Octahedral Fractal via Random Spin-State Jumps

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
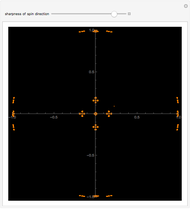
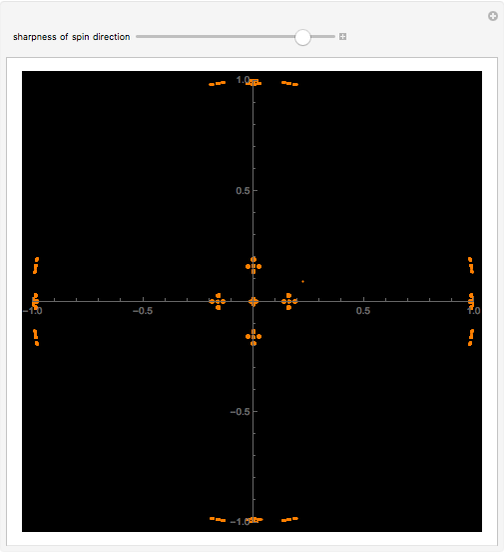
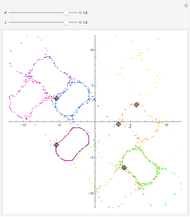
Quantum jumps of spin 1/2 states on the Bloch sphere are realized by Möbius transformations. Chaos games produced by a random sequence of six noncommuting transformations centered at the vertices of the octahedron result in a fractal pattern on the sphere. The parameter  ,
,  , defines the sharpness of the spin-direction measurements.
, defines the sharpness of the spin-direction measurements.
Contributed by: Arkadiusz Jadczyk (March 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The algorithm for computing Platonic quantum fractals in general: define 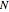 vertices
vertices 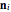 of a regular polyhedron (there are five Platonic solids). Choose a fixed parameter
of a regular polyhedron (there are five Platonic solids). Choose a fixed parameter  ,
,  , which defines the "sharpness" of the fractal. Then select a random starting point
, which defines the "sharpness" of the fractal. Then select a random starting point  on the unit sphere. Randomly select a vertex index
on the unit sphere. Randomly select a vertex index 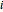 ; let
; let 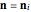 (one of the
(one of the 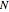 possible vertices). Apply the transformation
possible vertices). Apply the transformation
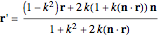 .
.
This is a Möbius transformation. It gives a new starting point on the sphere. Iterate the algorithm 10000 or more times.
Plot the first two coordinates of each point. The Möbius transformation theoretically maps the unit sphere onto itself. Yet after many iterations due to numerical inaccuracies, the norm  can start to diverge. Therefore, it is better to normalize
can start to diverge. Therefore, it is better to normalize  after each transformation.
after each transformation.
For more details about Platonic quantum fractals, see [1] and [2].
References
[1] A. Jadczyk and R. Oberg, "Quantum Jumps, EEQT and the Five Platonic Fractals." arxiv.org/abs/quant-ph/0204056.
[2] A. Jadczyk, Quantum Fractals: From Heisenberg's Uncertainty to Barnsley's Fractality, New Jersey: World Scientific 2014.
Permanent Citation