Quantum Random Walk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
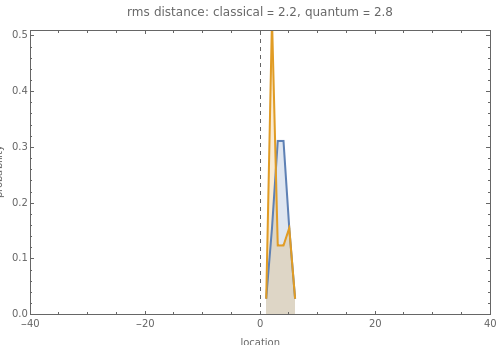
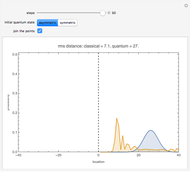
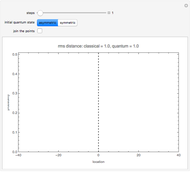
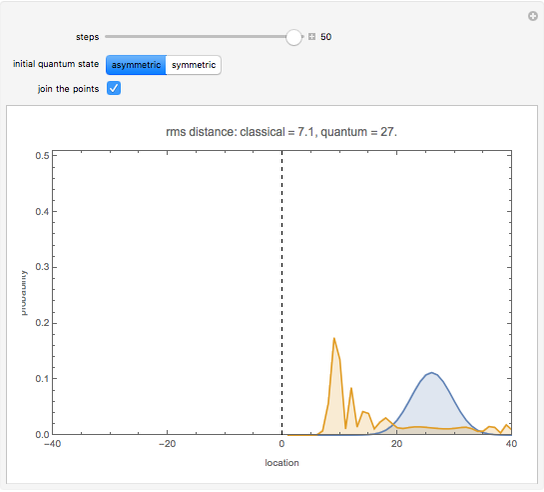
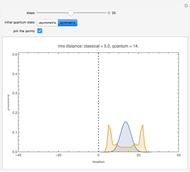
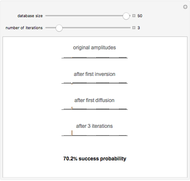
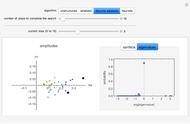
This Demonstration shows the probability distribution for discrete classical and quantum random walks on a line, starting from the location marked 0. The controls vary the number of steps for the walk and, for the quantum case, whether the initial state is symmetric or not. The plot label gives the root mean square (rms) distance of the walk from the origin after the specified number of steps.
Contributed by: Tad Hogg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
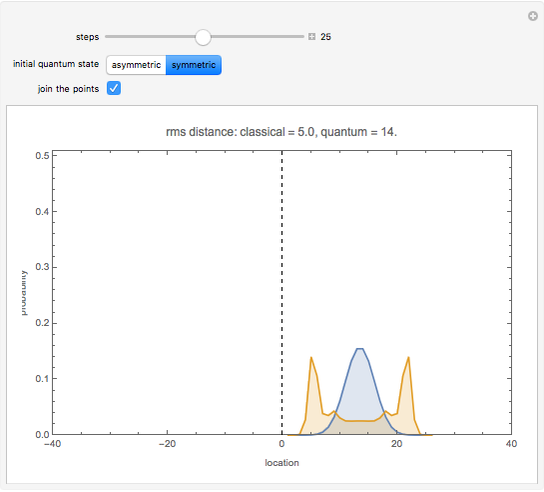
Snapshot 1: with the symmetric initial state, the probability for the quantum walk is symmetric about the origin
Snapshot 2: after many steps, the particle performing a quantum random walk is likely to be much farther from the origin than with a classical random walk
Snapshot 3: after just one step, both classical and quantum random walks have the same probabilities: equally likely to be at positions +1 or -1
In the classical random walk, at each step there is equal probability for the particle to move one unit to the left or right along the line. During a single random walk, the particle is at a definite location after each step. The probability shown in the plot is the fraction of such walks in which the particle is at each location after the specified number of steps.
In the quantum random walk, the particle is in a superposition of locations along the line. The values shown in the plot are the probability of finding the particle at each location if the particle is observed after the specified number of steps.
The state of the quantum particle after  steps can be expressed as a sum
steps can be expressed as a sum 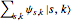 , where the
, where the 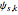 values are complex numbers,
values are complex numbers,  is an integer between
is an integer between 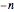 and
and  giving the location along the line, and
giving the location along the line, and  is a single quantum bit (called a qubit) that represents the value of a coin flipped to determine the direction of the particle at the next step: 0 and 1 correspond to decreasing and increasing
is a single quantum bit (called a qubit) that represents the value of a coin flipped to determine the direction of the particle at the next step: 0 and 1 correspond to decreasing and increasing  by 1, respectively. The probability of observing the particle at location
by 1, respectively. The probability of observing the particle at location  is
is  .
.
After a step, the superposition 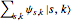 becomes
becomes 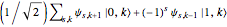 . Thus a quantum particle starting at a definite location
. Thus a quantum particle starting at a definite location 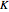 has equal probability of being observed after one step at locations
has equal probability of being observed after one step at locations 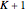 or
or 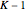 , the same as the classical random walk. But after more than one step, interference among multiple terms in the superposition gives different behavior between the classical and quantum random walks.
, the same as the classical random walk. But after more than one step, interference among multiple terms in the superposition gives different behavior between the classical and quantum random walks.
The behavior of the quantum random walk varies with the choice of initial state for the qubit  . This qubit can start with a definite state (0 or 1), the same as a classical bit. More generally, the qubit can start as a superposition of the two values 0 and 1. This Demonstration shows two examples for the initial state of the qubit. The asymmetric initial condition has
. This qubit can start with a definite state (0 or 1), the same as a classical bit. More generally, the qubit can start as a superposition of the two values 0 and 1. This Demonstration shows two examples for the initial state of the qubit. The asymmetric initial condition has 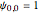 and all other values equal to zero. The symmetric initial condition has
and all other values equal to zero. The symmetric initial condition has 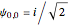 ,
, 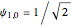 , and all other values equal to zero. In both cases, the particle starts at location 0, the same as for the classical random walk.
, and all other values equal to zero. In both cases, the particle starts at location 0, the same as for the classical random walk.
After an even or odd number of steps, the particle can only be at even or odd locations along the line, respectively. Selecting the "join the points" control shows a curve connecting the nonzero probabilities.
For further details and generalizations, see J. Kempe, "Quantum Random Walks: An Introductory Overview," Contemporary Physics, 44, 2003 pp. 307–327.
For a physical implementation, see M. Karski et al., "Quantum Walk in Position Space with Single Optically Trapped Atoms," Science, 325, 2009 pp. 174–177.
Permanent Citation