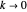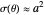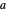Quantum Scattering by a Rigid Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
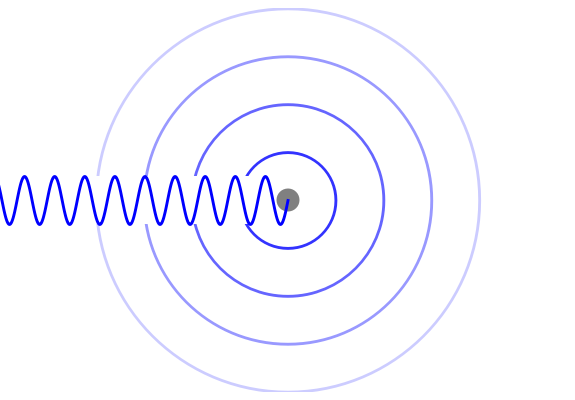
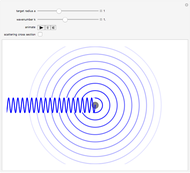
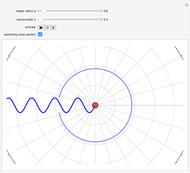
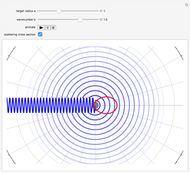
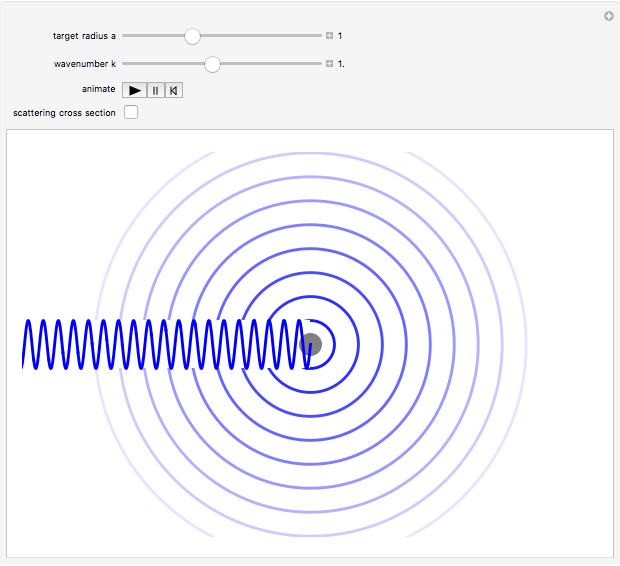
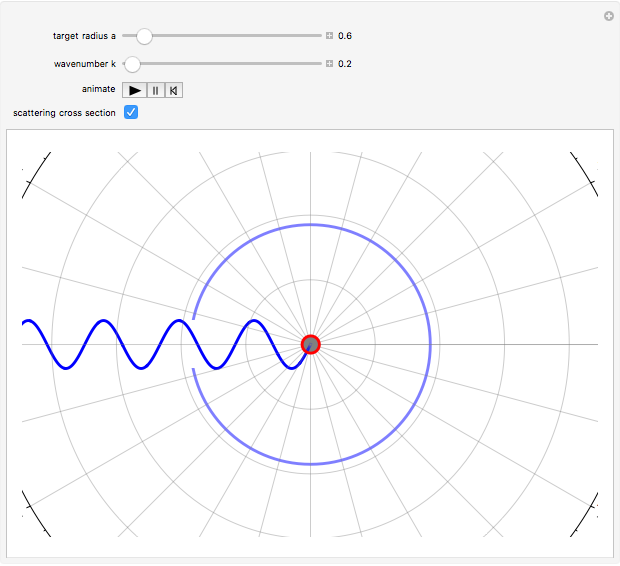
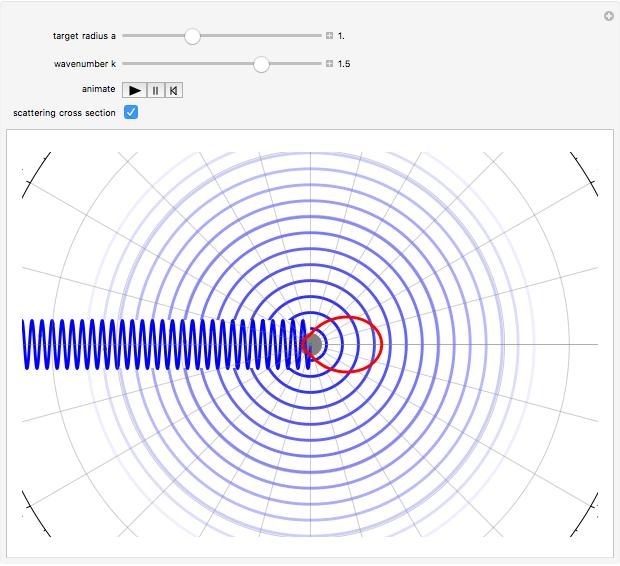
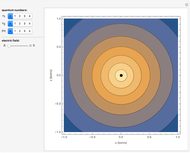
Consider the quantum-mechanical treatment of scattering in three dimensions by a spherically symmetrical potential centered at the origin. A standard problem is scattering by a rigid sphere, defined by the potential-energy function:  for
for  ,
, 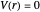 for
for  . For any spherically symmetrical potential, the asymptotic behavior of the wavefunction can be represented by the Faxen–Holzmark formula
. For any spherically symmetrical potential, the asymptotic behavior of the wavefunction can be represented by the Faxen–Holzmark formula 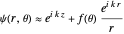 , where the first term represents an incoming plane wave in the positive
, where the first term represents an incoming plane wave in the positive  direction (
direction ( ) and the second term is an outgoing spherical wave from the scattering center. The scattering amplitude
) and the second term is an outgoing spherical wave from the scattering center. The scattering amplitude  determines the angular distribution of the outgoing wave. The differential scattering cross section is given by
determines the angular distribution of the outgoing wave. The differential scattering cross section is given by 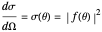 . A spherical-harmonic expansion of the plane wave,
. A spherical-harmonic expansion of the plane wave, 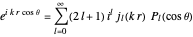 , reduces the outgoing wave to a sum of partial waves, the so-called partial wave expansion. The
, reduces the outgoing wave to a sum of partial waves, the so-called partial wave expansion. The  component is known as the
component is known as the  -wave, the
-wave, the  component, the
component, the  -wave, and so on. In practice, only a small number partial waves need be considered for a sufficiently accurate representation of the scattering, at least at low energies. The defining parameter of a partial wave is its phase shift
-wave, and so on. In practice, only a small number partial waves need be considered for a sufficiently accurate representation of the scattering, at least at low energies. The defining parameter of a partial wave is its phase shift 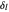 . For scattering by a rigid sphere,
. For scattering by a rigid sphere, 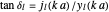 . In the preceding formulas,
. In the preceding formulas, 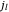 and
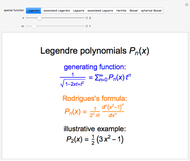
and  are spherical Bessel functions of the first and second kind, while
are spherical Bessel functions of the first and second kind, while 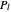 is a Legendre polynomial.
is a Legendre polynomial.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: This topic is treated in most quantum-mechanics textbooks, notably those of Schiff, Merzbacher, and Landau–Lifshitz.
Permanent Citation