Quantum Teleportation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
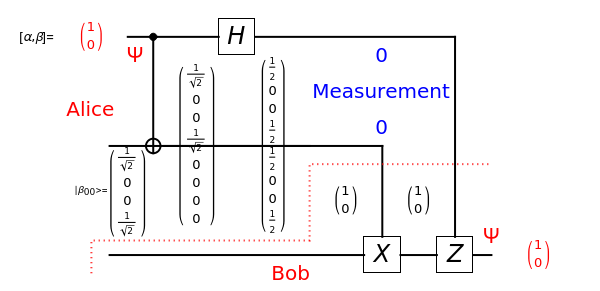
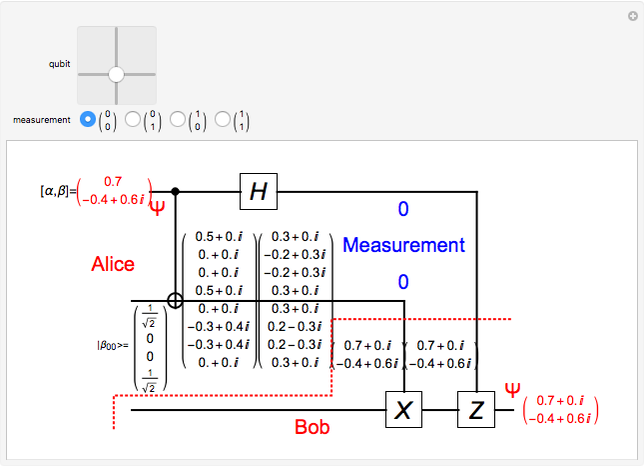
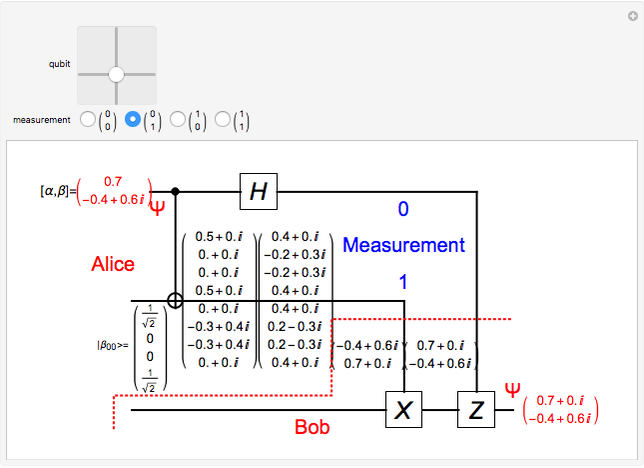
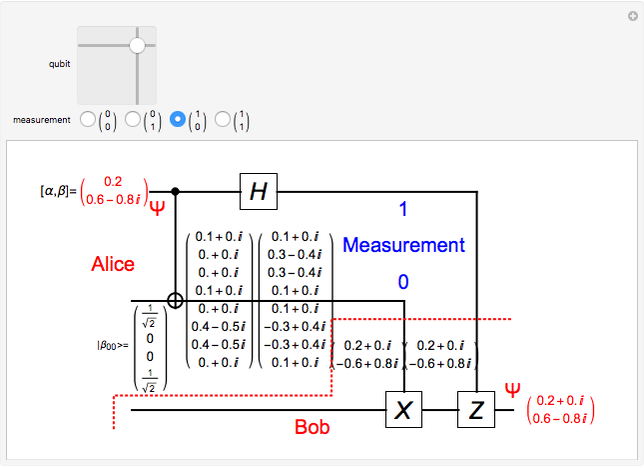
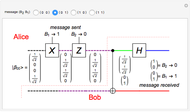
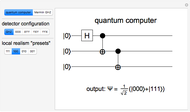
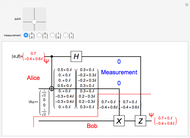
In quantum teleportation, a sender (Alice) can send the state of one quantum bit (qubit) to the receiver (Bob). The input to the circuit is the qubit  whose state is to be transported, along with one of a pair of qubits entangled in the Bell basis state (the upper qubit). The other qubit from the Bell pair (the lower qubit) is sent unchanged to Bob. Alice process her two qubits with two quantum gates and measures the output (controlled by the user) yielding two classical bits, which are sent back to Bob. Bob then uses these bits to control the processing on his qubit from the entangled Bell pair through two quantum gates, and this yields a qubit with the same state Alice teleported.
whose state is to be transported, along with one of a pair of qubits entangled in the Bell basis state (the upper qubit). The other qubit from the Bell pair (the lower qubit) is sent unchanged to Bob. Alice process her two qubits with two quantum gates and measures the output (controlled by the user) yielding two classical bits, which are sent back to Bob. Bob then uses these bits to control the processing on his qubit from the entangled Bell pair through two quantum gates, and this yields a qubit with the same state Alice teleported.
Contributed by: Brad Rubin (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
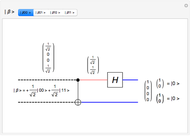
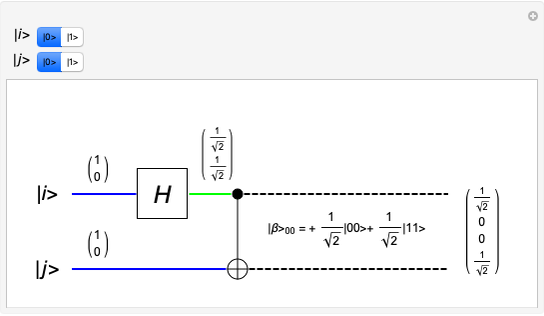
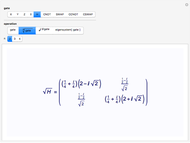
A quantum bit (qubit) cannot be cloned or copied, but its state can be teleported. In quantum teleportation, a sender (Alice) can send the state of one quantum bit (qubit) to the receiver (Bob). The input to the circuit is the qubit whose state is transported (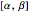 in the diagram), represented by two complex numbers specified by the user via the 2D slider), along with one of a pair of qubits entangled in the Bell basis state (the upper qubit). (See the Demonstration Measuring Entangled Qubits for more detail on the Bell basis state and quantum gates.) The other qubit from the pair (the lower qubit) is sent unchanged to Bob. Processing Alice's two qubits, first with a CNOT gate and then with a Hadamard gate, yields two qubits that are then measured. The act of measuring causes the quantum state to collapse, yielding two classical (0 or 1) bits. There are four randomly possible outcomes of this measurement of the two qubits (00, 01, 10, 11), which can be chosen by the user via the radio buttons, simulating the random outcome. An interesting thing about this circuit is that it does not matter what the specific measurement outcome is, because the teleported qubit output will turn out to be the same, independent of the measurement. The measurement output classical bits are sent to Bob, who uses these bits to control the processing on his entangled qubit pair with a Pauli X (or NOT) operation and a Pauli Z (or Phase Flip) operation, yielding the teleported qubit state
in the diagram), represented by two complex numbers specified by the user via the 2D slider), along with one of a pair of qubits entangled in the Bell basis state (the upper qubit). (See the Demonstration Measuring Entangled Qubits for more detail on the Bell basis state and quantum gates.) The other qubit from the pair (the lower qubit) is sent unchanged to Bob. Processing Alice's two qubits, first with a CNOT gate and then with a Hadamard gate, yields two qubits that are then measured. The act of measuring causes the quantum state to collapse, yielding two classical (0 or 1) bits. There are four randomly possible outcomes of this measurement of the two qubits (00, 01, 10, 11), which can be chosen by the user via the radio buttons, simulating the random outcome. An interesting thing about this circuit is that it does not matter what the specific measurement outcome is, because the teleported qubit output will turn out to be the same, independent of the measurement. The measurement output classical bits are sent to Bob, who uses these bits to control the processing on his entangled qubit pair with a Pauli X (or NOT) operation and a Pauli Z (or Phase Flip) operation, yielding the teleported qubit state 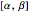 . The matrices show the intermediate qubit states as the circuit processing progresses.
. The matrices show the intermediate qubit states as the circuit processing progresses.
References:
P. Kaye, R. Laflamme, and M. Mosca, An Introduction to Quantum Computing, New York: Oxford University Press, 2007.
C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wooters, "Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels," Physical Review Letters, 70, 1993 pp. 1895–1899.
Permanent Citation