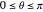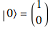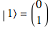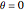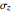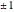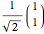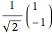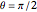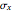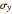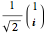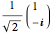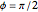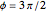Qubits on the Poincaré (Bloch) Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
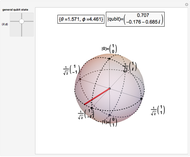
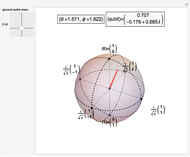
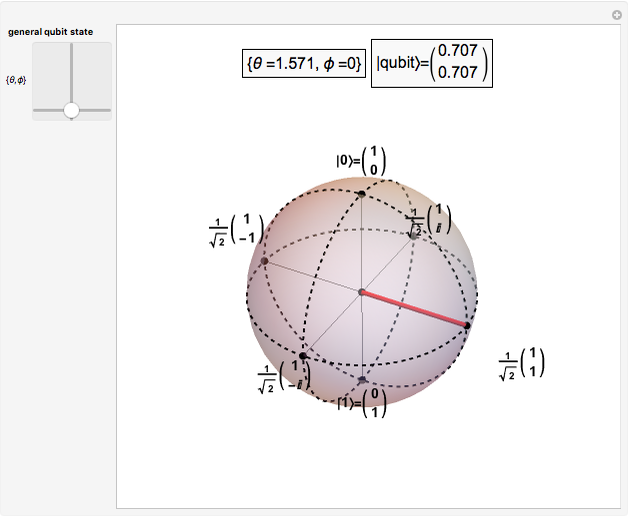
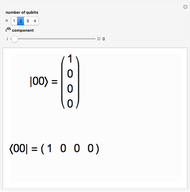
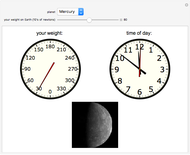
The Poincaré (Bloch) sphere provides a geometric representation of a pure qubit (quantum bit) state space as points on the surface of the unit sphere 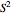 . Any point of the surface represents some pure qubit. The mixed qubit states can be represented by points inside of the unit sphere, with the maximally mixed state laying at the center. The red line from the center to the surface of the sphere corresponds to the pure state and has unit length. For mixed qubit state the length of line must be less than 1.
. Any point of the surface represents some pure qubit. The mixed qubit states can be represented by points inside of the unit sphere, with the maximally mixed state laying at the center. The red line from the center to the surface of the sphere corresponds to the pure state and has unit length. For mixed qubit state the length of line must be less than 1.
Contributed by: Rudolf Muradian (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
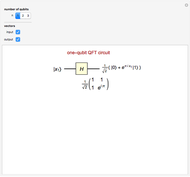
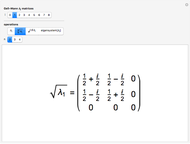
The Pauli spin operators are defined as 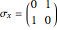 ,
, 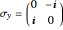 ,
,  . The three directions
. The three directions  ,
,  , and
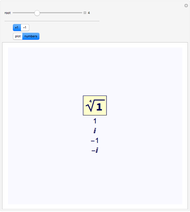
, and 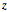 correspond to the diagonal, circular, and computational bases. The most general qubit state
correspond to the diagonal, circular, and computational bases. The most general qubit state 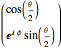 is an eigenvector of the operator
is an eigenvector of the operator 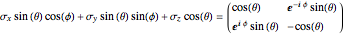 with eigenvalue 1. The Bloch vector is a unit vector connecting the origin to a point
with eigenvalue 1. The Bloch vector is a unit vector connecting the origin to a point 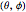 with Cartesian coordinates (
with Cartesian coordinates (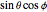 ,
, 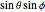 ,
, 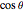 ).
).
Permanent Citation