Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

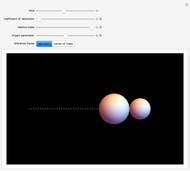
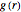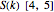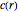Radial Distribution Function for Hard Spheres

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

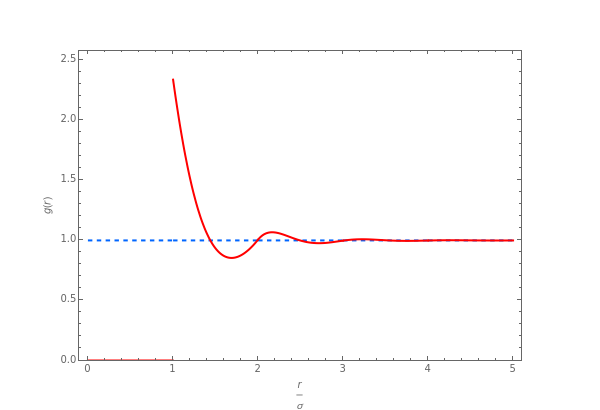
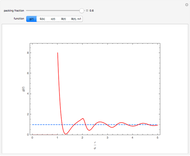
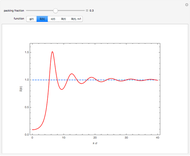
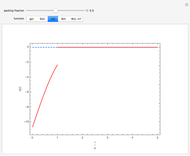
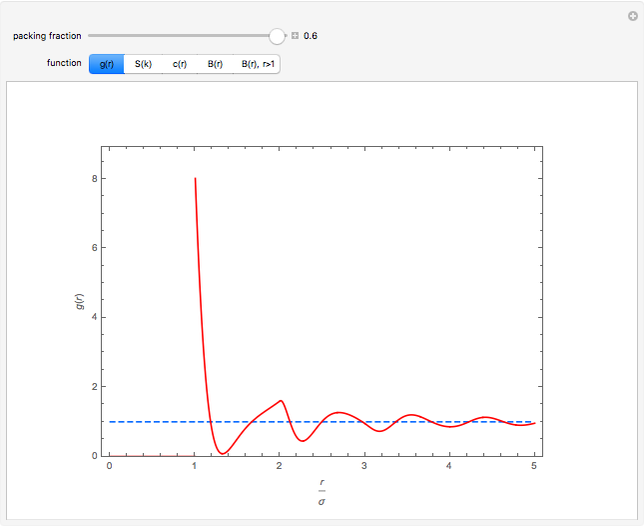
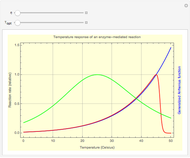
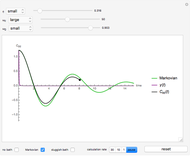
In statistical mechanics, the distribution of interparticle separations determines the radial distribution function [1].

[more]

This Demonstration shows the radial distribution function of a three-dimensional liquid composed of identical hard spheres of diameter , making use of the exact solution of the Percus–Yevick integral equation [2, 3]. You can vary the packing fraction of the liquid, that is, the fraction of the total volume occupied by the spheres themselves. For a packing fraction greater than about 0.49, the corresponding can be regarded as that of a metastable liquid since the true stable phase is a crystal.

The Demonstration also includes three functions directly related to the radial distribution function : the structure factor , the direct correlation function [6], and the bridge function [7].

[less]

Contributed by: Andrés Santos (May 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

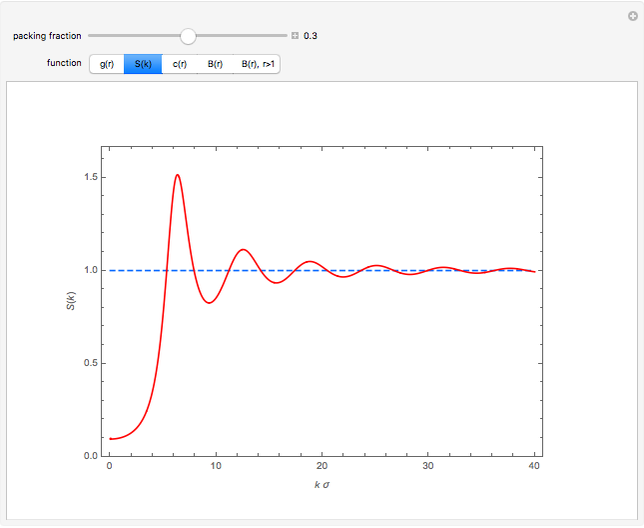
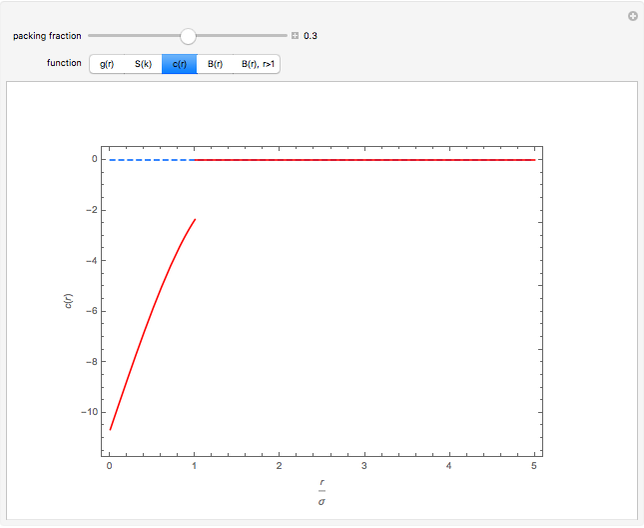
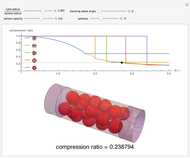
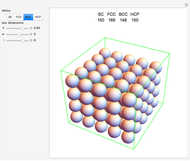
The exact solution of the Percus–Yevick integral equation for hard spheres was first obtained in [2] and [3]. The entirely analytic forms for the static structure factor 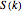were first presented in [4].

References

[1] Wikipedia. "Radial Distribution Function." (Mar 8, 2013) en.wikipedia.org/wiki/Radial_distribution_function.

[2] M. S. Wertheim, "Exact Solution of the Percus–Yevick Integral Equation for Hard Spheres," Physical Review Letters, 10(8), 1963 pp. 321–323. doi:10.1103/PhysRevLett.10.321.

[3] E. Thiele, "Equation of State for Hard Spheres," The Journal of Chemical Physics, 39(2), 1963 pp. 474–479. doi:10.1063/1.1734272.

[4] N. W. Ashcroft and J. Lekner, "Structure and Resistivity of Liquid Metals," Physical Review, 145(1), 1966 pp. 83–90.

[5] Wikipedia. "Structure factor." (May 9, 2013) en.wikipedia.org/wiki/Structure_factor.

[6] Wikipedia. "Ornstein–Zernike equation." (April 20, 2013) en.wikipedia.org/wiki/Ornstein% E2 %80 %93 Zernike_equation.

[7] SklogWiki. "Bridge function." (November 7, 2012) www.sklogwiki.org/SklogWiki/index.php/Bridge_function.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send