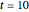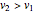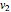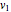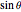Radiation Pulse from an Accelerated Point Charge

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
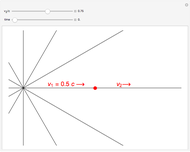
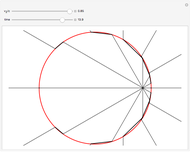
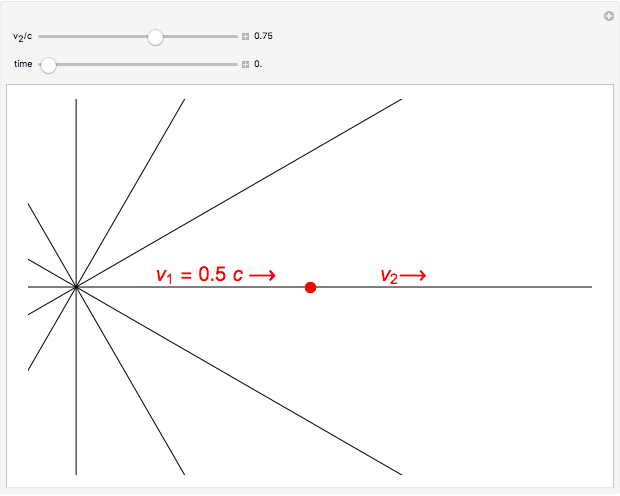
J. J. Thomson first suggested a pictorial representation of how an instantaneously accelerated point charge can produce a pulse of electromagnetic radiation. An electron, with charge  , moving at a constant speed
, moving at a constant speed  , even when a significant fraction of the speed of light
, even when a significant fraction of the speed of light  , produces an electric field of magnitude
, produces an electric field of magnitude  , (add factor
, (add factor 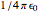 if you cannot live without SI units), where
if you cannot live without SI units), where 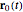 represents the projected position of the source charge at time
represents the projected position of the source charge at time  , assuming that it continues to move at constant speed
, assuming that it continues to move at constant speed  from its position
from its position  at the retarded time
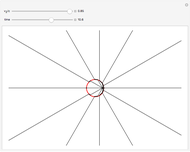
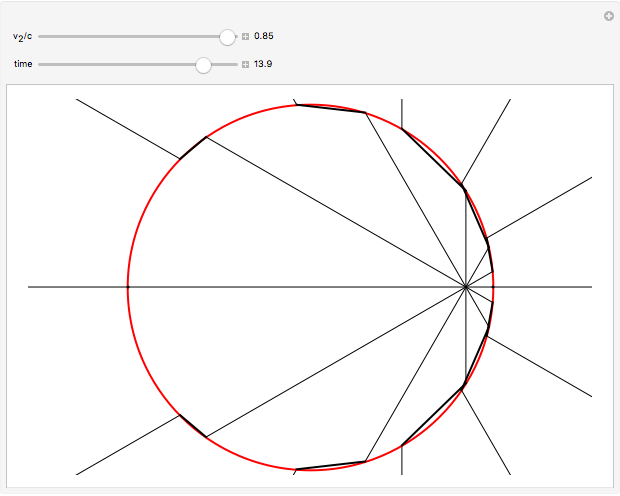
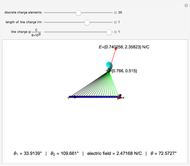
at the retarded time 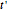 . This is derived most lucidly in the Feynman Lectures [1]. Thus a uniformly moving point source emits a spherical longitudinal electric field, although its magnitude does vary with direction. This is represented in the graphic by a series of 12 uniformly spaced radial spokes.
. This is derived most lucidly in the Feynman Lectures [1]. Thus a uniformly moving point source emits a spherical longitudinal electric field, although its magnitude does vary with direction. This is represented in the graphic by a series of 12 uniformly spaced radial spokes.
Contributed by: S. M. Blinder (May 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. II, Reading, MA: Addison–Wesley, 1964, pp. 26.1–26.4.
[2] E. M. Purcell, Electricity and Magnetism: Berkeley Physics Course, Vol. 2, New York: McGraw-Hill, 1984, pp. 331–334.
[3] D. V. Schroeder, "Purcell Simplified or Electricity, Magnetism, and Relativity." (January 1999) http://physics.weber.edu/schroeder/mrr/MRRtalk.html.
Permanent Citation