Details

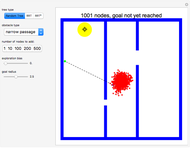
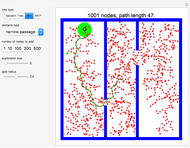
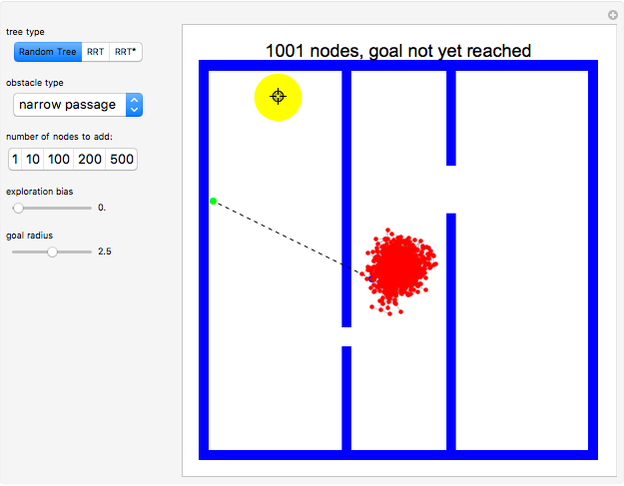
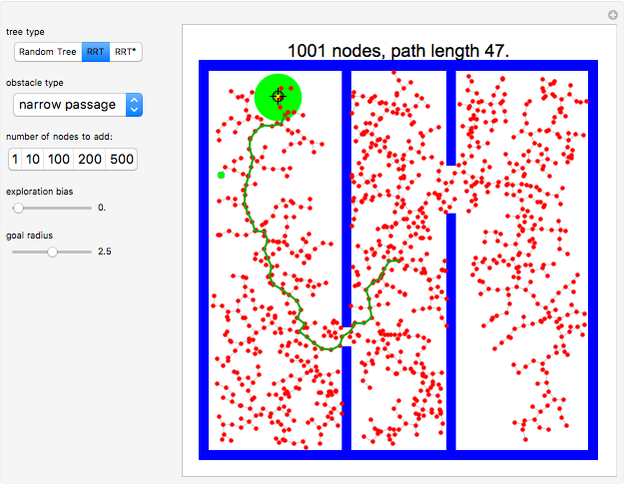
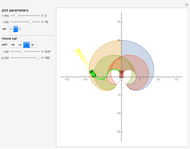
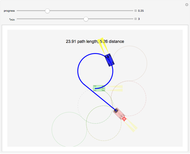
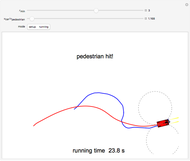
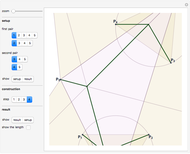
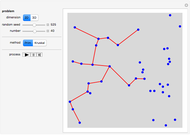
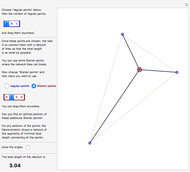
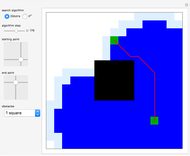
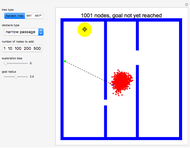
This Demonstration shows a tree defined by red nodes with black edges. Obstacles are drawn in blue, and the goal position is indicated by a locator surrounded by a disc of radius goal radius. This is yellow before the goal is reached and turns green after success. As shown in the Snapshots, a tree generated by random motion from a randomly selected tree node does not explore very far (Snapshot 1). A rapidly exploring random tree (RRT) first selects a goal point (drawn in green), then tries to add an edge from the closest node in the tree (blue) toward the goal point. This results in a tree that tends to quickly explore the space, because search is biased into the largest Voronoi regions of a graph defined by the tree. RRT* improves on this by rewiring the tree to form shortest paths. RRT* converges to the shortest path, at the cost of more computation. All three trees are probabilistically complete, meaning if a nonzero width path exists, the tree will eventually find the path. This Demonstration attempts to construct a path (dark green) from the starting point (red) to the goal locator. Exploration can be biased toward the goal instead of random sampling by changing the corresponding slider.

In this Demonstration, each node on the tree has a tooltip that reports the total distance to this node from the root node at 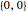. In general, the path lengths for RRT* are shorter than RRT. Try changing the obstacle type, the tree type and the goal location.

RRTs were developed by S. M. LaValle and J. J. Kuffner Jr. in [1] and [2]. They are often used for robot motion planning, especially for high-dimensional problems with obstacles. The RRT* variant was introduced by S. Karaman and E. Frazolli [3].

References

[1] S. M. LaValle, Rapidly-Exploring Random Trees: A New Tool for Path Planning, Computer Science Department, Iowa State University (TR 98-11), 1998.

[2] S. M. LaValle and J. J. Kuffner, Jr., "Randomized Kinodynamic Planning," The International Journal of Robotics Research, 20(5), 2001 pp. 378–400. doi:10.1177/02783640122067453.

[3] S. Karaman and E. Frazzoli, "Sampling-Based Algorithms for Optimal Motion Planning," The International Journal of Robotics Research, 30(7), 2011 pp. 846–894. doi:10.1177/0278364911406761.

[4] Wikipedia. "Rapidly-Exploring Random Tree." (Jan 11, 2018) en.wikipedia.org/wiki/Rapidly-exploring_random _tree.