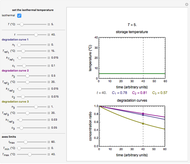
Reaction Rate Dependence on Temperature and Moisture During Storage

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
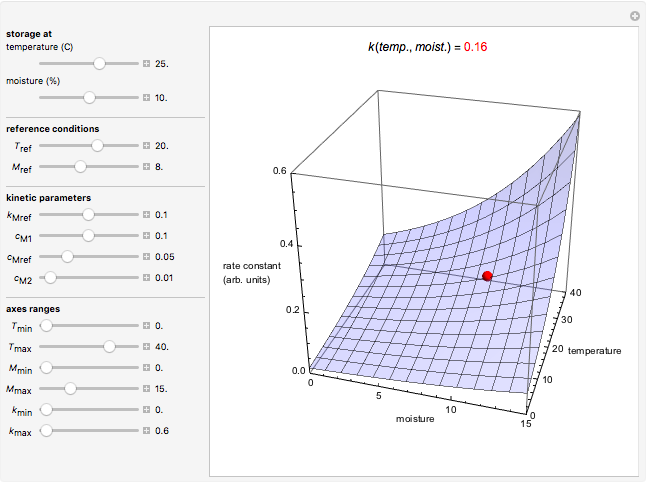
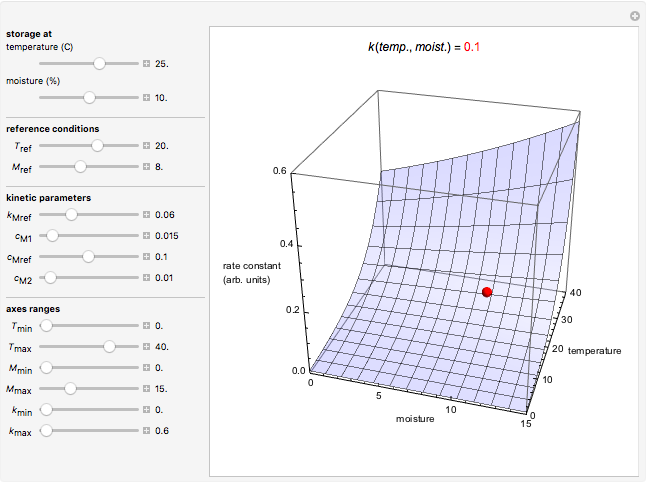
For chemical reactions and many biological processes in stored dried foods, the reaction rates depend on both the temperature and water activity, the latter determined by the moisture content. This dependence can be visualized in a 3D plot of rate constant-temperature-moisture content values, with their relationship generated with a nested model. It is assumed that the temperature dependence of the isothermal rate constant follows the exponential model, a simpler alternative to the Arrhenius equation, for which the two parameters for moisture dependence follow a similar type of exponential dependence.
Contributed by: Mark D. Normand and Micha Peleg (August 2018)
Open content licensed under CC BY-NC-SA
Details
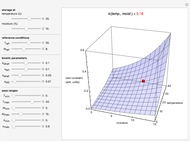
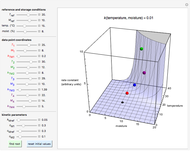
Snapshot 1: rate constant-temperature-moisture content relationship of a hypothetical reaction having low sensitivity to moisture content in the pertinent range
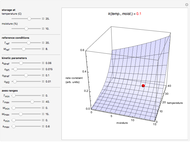
Snapshot 2: rate constant-temperature-moisture content relationship of a hypothetical reaction having high sensitivity to moisture content in the pertinent range
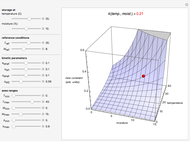
Snapshot 3: rate constant-temperature-moisture content relationship of a hypothetical reaction having low sensitivity to temperature in the pertinent range
Snapshot 4: rate constant-temperature-moisture content relationship of a hypothetical reaction having high sensitivity to temperature in the pertinent range
The temperature effect on the rate of chemical reactions and biological processes in dried foods has been described primarily using the Arrhenius equation, but also by several alternative models [1]. It has been shown that when the rate constant’s temperature dependence 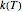 follows the Arrhenius equation, it can also be described by the simpler exponential model
follows the Arrhenius equation, it can also be described by the simpler exponential model
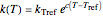 ,
,
where
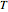 is the temperature in °C,
is the temperature in °C,
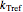 is the rate at a chosen reference temperature
is the rate at a chosen reference temperature 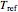 , also in °C and
, also in °C and
 is a constant having
is a constant having 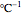 units [2].
units [2].
Reported isothermal moisture-dependence relationships  versus
versus 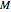 show that within the range pertinent to dried food storage, they resemble those of the temperature [3, 4], in which case they can be described by a similar exponential model, at least as a first-order approximation.
show that within the range pertinent to dried food storage, they resemble those of the temperature [3, 4], in which case they can be described by a similar exponential model, at least as a first-order approximation.
Assuming that the moisture-dependence of the model's temperature parameters  and
and  both follow the exponential model, albeit having different parameters, they can be described by
both follow the exponential model, albeit having different parameters, they can be described by
and
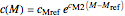 ,
,
where
 is the moisture content on dry or wet basis,
is the moisture content on dry or wet basis,
 is a reference moisture content on the same basis as
is a reference moisture content on the same basis as  and
and
 ,
, 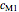 ,
, 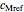 and
and 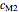 are constants characteristic of the food being considered.
are constants characteristic of the food being considered.
Inserting the 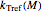 and
and 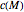 terms so defined into the
terms so defined into the 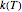 equation produces the four-parameter nested model of the rate constant-temperature-moisture relationship:
equation produces the four-parameter nested model of the rate constant-temperature-moisture relationship:
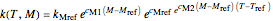 .
.
This Demonstration generates and displays rate constant versus temperature and moisture relationships in the form of 3D plots using the given 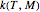 equation as a model, with the reference temperature
equation as a model, with the reference temperature 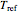 and moisture
and moisture  , as well as the
, as well as the 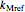 ,
, 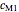 ,
, 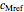 and
and 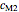 parameters and axes ranges entered by sliders. We also calculate and display the numerical value of
parameters and axes ranges entered by sliders. We also calculate and display the numerical value of 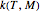 for
for 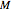 and
and  values selected with sliders.
values selected with sliders.
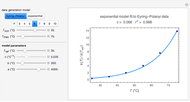
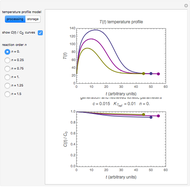
The primary purpose of this Demonstration is to visualize the nested  model, not to match that of any specific reaction in a particular food. Therefore, not all the parameter-combinations allowed by the controls necessarily represent real-life scenarios. However, if the model's parameters
model, not to match that of any specific reaction in a particular food. Therefore, not all the parameter-combinations allowed by the controls necessarily represent real-life scenarios. However, if the model's parameters 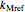 ,
, 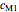 ,
, 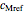 and
and 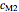 have been obtained from experimental
have been obtained from experimental 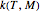 data by regression, then the Demonstration can be used as a calculator for new
data by regression, then the Demonstration can be used as a calculator for new 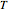 and
and 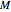 combinations in an appropriate temperature-moisture range.
combinations in an appropriate temperature-moisture range.
References
[1] C. S. Barsa, M. D. Normand and M. Peleg, "On Models of the Temperature Effect on the Rate of Chemical Reactions and Biological Processes in Foods," Food Engineering Reviews, 4(4), 2012 pp. 191–202. doi:10.1007/s12393-012-9056-x.
[2] M. Peleg, M. D. Normand and M. G. Corradini, "The Arrhenius Equation Revisited," Critical Reviews in Foods Science and Nutrition, 52(9), 2012 pp. 830–851. doi:10.1080/10408398.2012.667460.
[3] K. Di Scala and G. Crapiste, "Drying Kinetics and Quality Changes During Drying of Red Peppers," LWT - Food Science and Technology, 41(5), 2008 pp. 789–795. doi:10.1016/j.lwt.2007.06.007.
[4] J. Qiu, J.-E. Vuist, R. M. Boom and M. A. I. Schutyser, "Formation and Degradation Kinetics of Organic Acids During Heating and Drying of Concentrated Tomato Juice," LWT - Food Science and Technology, 87(1), 2018 pp. 112–121. doi:10.1016/j.lwt.2017.08.081.
Snapshots
Permanent Citation