Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Real Options

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

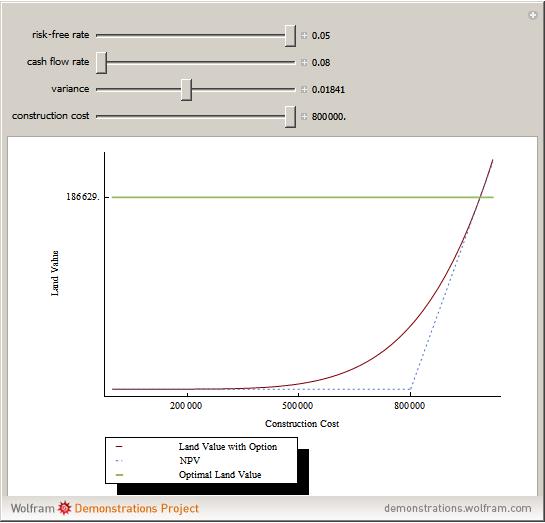
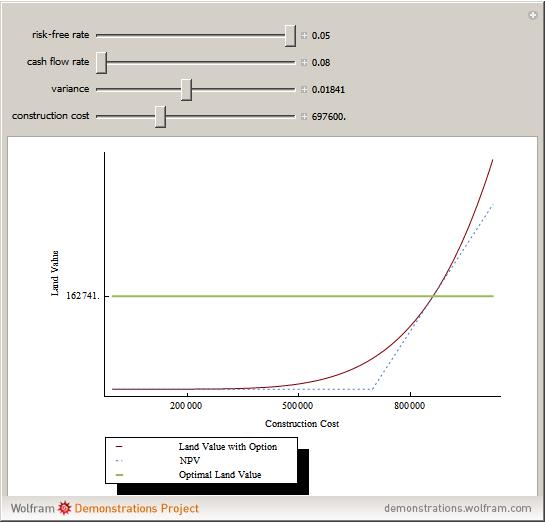
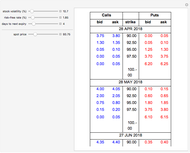
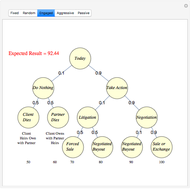
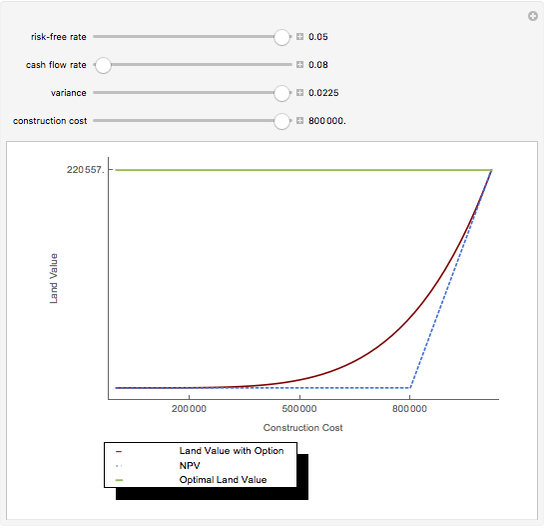
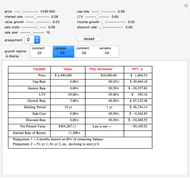
A number of characteristics differentiate real options from financial options. A real option restricts the owner's rights to a specific property at a specific location; the exercise of a real option affects the owner and usually is either irreversible or reversible only at prohibitive cost. Real options, such as development prior to a zoning change that forbids building, may be passive, imposed by outsiders, or exercised by the passing of time without the property owner's action or consent. Mathematically, real options differ from financial options in that the equations used to value options require precise valuations at different points in time and a crucial value for uncertainty (often modeled as variance) that, while generally available for securities, is virtually impossible to secure from real estate markets.

[more]

With all of these difficulties, the study of real options is still important as a way to think about real estate investment, especially undeveloped land. This analysis describes how land in its undeveloped state may be more valuable in that state while the option remains unexercised. During that time the difference in the two plots illustrates how net present value analysis fails to include option value. This Demonstration shows the way option value and net present value converge to optimize land value and how changes in the input variables change that convergence.

[less]

Contributed by: Roger J. Brown (March 2011)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA

Snapshots

Details

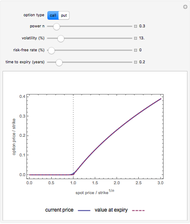
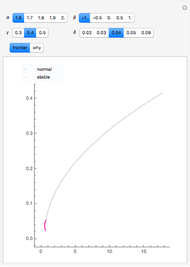
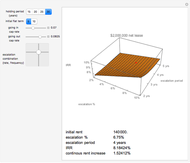
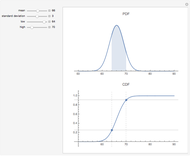
Consistent with option theory, option value increases with higher uncertainty.

Equations, generally known as the Samuelson–McKean formulas, feature an option elasticity measure that captures the percentage change in the value of the option with each one percent change in the value of the underlying asset.

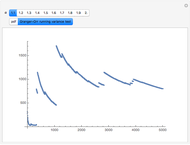
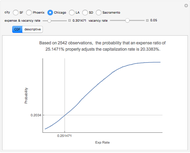
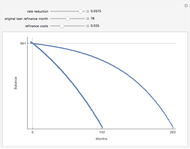
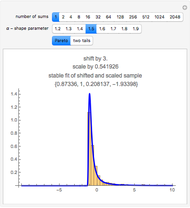
In the search for an appropriate value for the variance, one should consider volatility of individual properties rather than that of a portfolio of properties, such as a REIT.

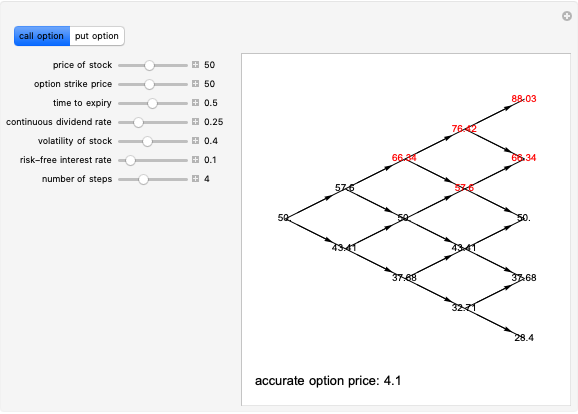
Equations for the redevelopment option differ due to the fact that some income is collected during the option period.

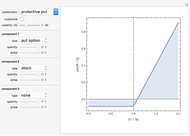
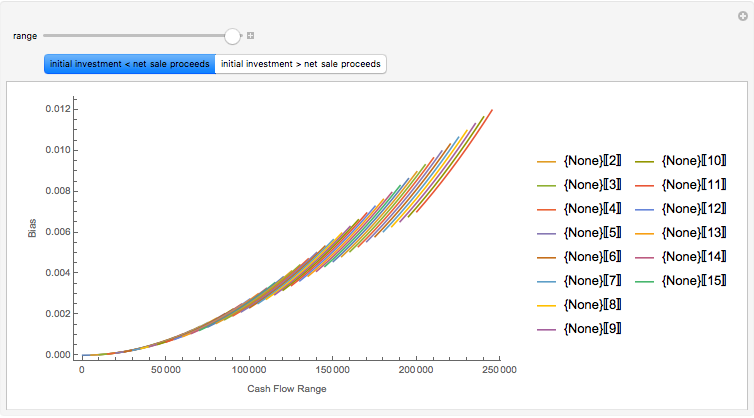
The most common option in real estate—not illustrated here—is the put option associated with nonrecourse financed home ownership. Essentially, the homeowner has a recurring monthly embedded option to "walk away" and "put" the property on the lender at the loan balance.

A. K. Dixit and R. S. Pindyck, Investment under Uncertainty, Princeton, NJ: Princeton University Press, 1994.

P. Samuelson, "Rational Theory of Warrant Pricing," Industrial Management Review, 6, 1965 pp. 41–50.

More information is available in chapter six of Private Real Estate Investment and at mathestate.com.

R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send