Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Reconstruction of the Great Wall

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Historically, the Great Wall stretches over approximately 6,400 km in total from Shanhai pass in the east to Jayu pass in the west, along a rough arc.

[more]

After hundreds of years of natural erosion and human activity, the Great Wall is vanishing. A survey shows 20% of it is in ruins and another 50% has already disappeared.

The existing locations of the Great Wall are shown as points. Their GPS positions come from Google Earth.

What is those points can tell us? What was the length of the Great Wall? How to estimate the history from the viewpoint of present?

This Demonstration shows a method for reconstructing the Great Wall by using a minimum spanning tree from the GPS points, giving a maximum distance of 6,104 km.

[less]

Contributed by: Frederick Wu (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

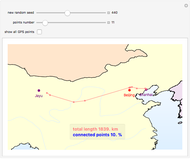
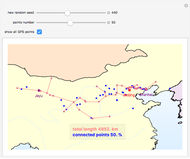
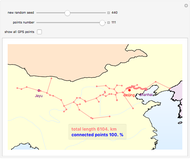
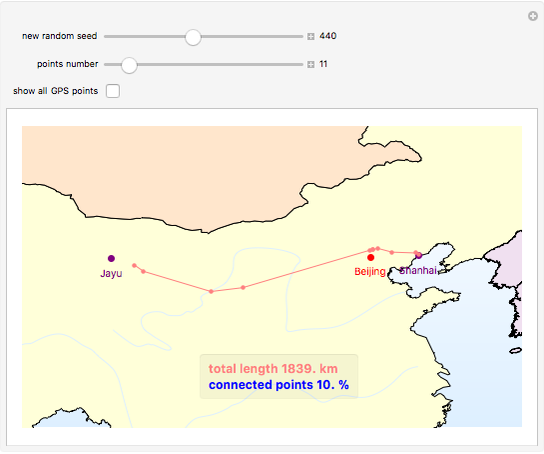
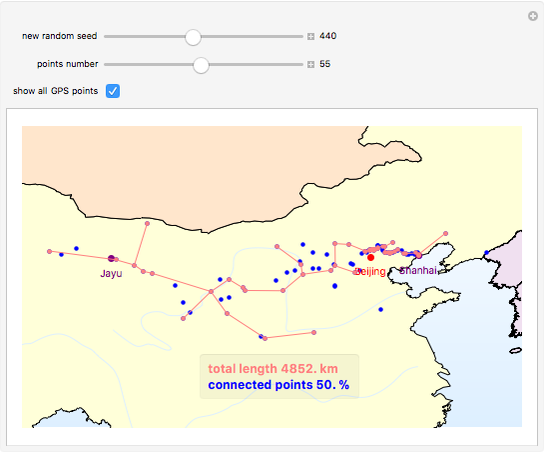
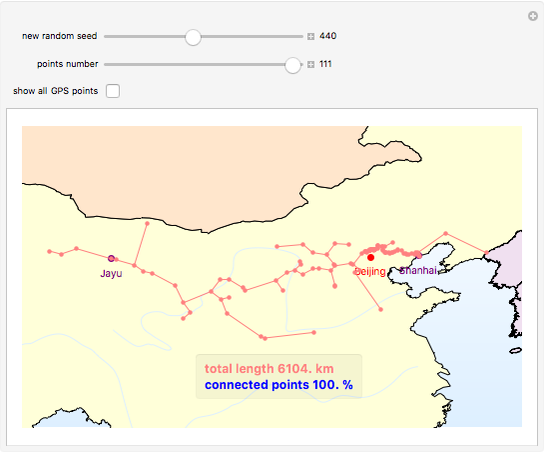
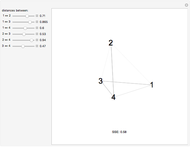
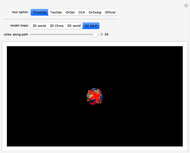
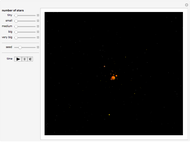
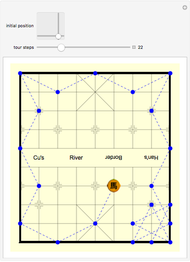
The graphics show randomly selected points connected using a minimum spanning tree by Kruskal's algorithm.

Snapshot 1: 11 random points (10% of the points) with a connected length of 1,839 km

Snapshot 2: 55 random points (50% of the points) with a connected length of 4,852 km

Snapshot 3: all 111 existing points (100% of the points) gives a total length of 6,104 km

The initial location data of the Great Wall is based on GPS coordinate points from Google Earth. Most of the existing GPS points are distributed to the north of Beijing.

For more details, see Chapter 6 of F. Wu, Manipulate@Mathematica, Beijing: Tsinghua, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send