Reconstruction of Vega's Prime Number Table

Initializing live version

show page

show number of primes

show page 92

show Gauss letter

page number

102001	102643	103451	104147	104801	105517	106273	106871	107693	108347
102013	102647	103457	104149	104803	105527	106277	106877	107699	108359
102019	102653	103471	104161	104827	105529	106279	106903	107713	108377
102023	102667	103483	104173	104831	105533	106291	106907	107717	108379
102031	102673	103511	104179	104849	105541	106297	106921	107719	108401
102043	102677	103529	104183	104851	105557	106303	106937	107741	108413
102059	102679	103549	104207	104869	105563	106307	106949	107747	108421
102061	102701	103553	104231	104879	105601	106319	106957	107761	108439
102071	102761	103561	104233	104891	105607	106321	106961	107773	108457
102077	102763	103567	104239	104911	105613	106331	106963	107777	108461
102079	102769	103573	104243	104917	105619	106349	106979	107791	108463
102101	102793	103577	104281	104933	105649	106357	106993	107827	108497
102103	102797	103583	104287	104947	105653	106363	107021	107837	108499
102107	102811	103591	104297	104953	105667	106367	107033	107839	108503
102121	102829	103613	104309	104959	105673	106373	107053	107843	108517
102139	102841	103619	104311	104971	105683	106391	107057	107857	108529
102149	102859	103643	104323	104987	105691	106397	107069	107867	108533
102161	102871	103651	104327	104999	105701	106411	107071	107873	108541
102181	102877	103657	104347	105019	105727	106417	107077	107881	108553
102191	102881	103669	104369	105023	105733	106427	107089	107897	108557
102197	102911	103681	104381	105031	105751	106433	107099	107903	108571
102199	102913	103687	104383	105037	105761	106441	107101	107923	108587
102203	102929	103699	104393	105071	105767	106451	107119	107927	108631
102217	102931	103703	104399	105097	105769	106453	107123	107941	108637
102229	102953	103723	104417	105107	105817	106487	107137	107951	108643
102233	102967	103769	104459	105137	105829	106501	107171	107971	108649
102241	102983	103787	104471	105143	105863	106531	107183	107981	108677
102251	103001	103801	104473	105167	105871	106537	107197	107999	108707
102253	103007	103811	104479	105173	105883	106541	107201	108007	108709
102259	103043	103813	104491	105199	105899	106543	107209	108011	108727
102293	103049	103837	104513	105211	105907	106591	107227	108013	108739
102299	103067	103841	104527	105227	105913	106619	107243	108023	108751
102301	103069	103843	104537	105229	105929	106621	107251	108037	108761
102317	103079	103867	104543	105239	105943	106627	107269	108041	108769
102329	103087	103889	104549	105251	105953	106637	107273	108061	108791
102337	103091	103903	104551	105253	105967	106649	107279	108079	108793
102359	103093	103913	104561	105263	105971	106657	107309	108089	108799
102367	103099	103919	104579	105269	105977	106661	107323	108107	108803
102397	103123	103951	104593	105277	105983	106663	107339	108109	108821
102407	103141	103963	104597	105319	105997	106669	107347	108127	108827
102409	103171	103967	104623	105323	106013	106681	107351	108131	108863
102433	103177	103969	104639	105331	106019	106693	107357	108139	108869
102437	103183	103979	104651	105337	106031	106699	107377	108161	108877
102451	103217	103981	104659	105341	106033	106703	107441	108179	108881
102461	103231	103991	104677	105359	106087	106721	107449	108187	108883
102481	103237	103993	104681	105361	106103	106727	107453	108191	108887
102497	103289	103997	104683	105367	106109	106739	107467	108193	108893
102499	103291	104003	104693	105373	106121	106747	107473	108203	108907
102503	103307	104009	104701	105379	106123	106751	107507	108211	108917
102523	103319	104021	104707	105389	106129	106753	107509	108217	108923
102533	103333	104033	104711	105397	106163	106759	107563	108223	108929
102539	103349	104047	104717	105401	106181	106781	107581	108233	108943
102547	103357	104053	104723	105407	106187	106783	107599	108247	108947
102551	103387	104059	104729	105437	106189	106787	107603	108263	108949
102559	103391	104087	104743	105449	106207	106801	107609	108271	108959
102563	103393	104089	104759	105467	106213	106823	107621	108287	108961
102587	103399	104107	104761	105491	106217	106853	107641	108289	108967
102593	103409	104113	104773	105499	106219	106859	107647	108293	108971
102607	103421	104119	104779	105503	106243	106861	107671	108301	108991
102611	103423	104123	104789	105509	106261	106867	107687	108343	109001

Download to Desktop

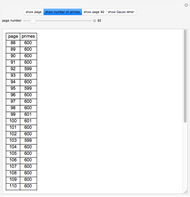
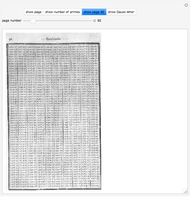
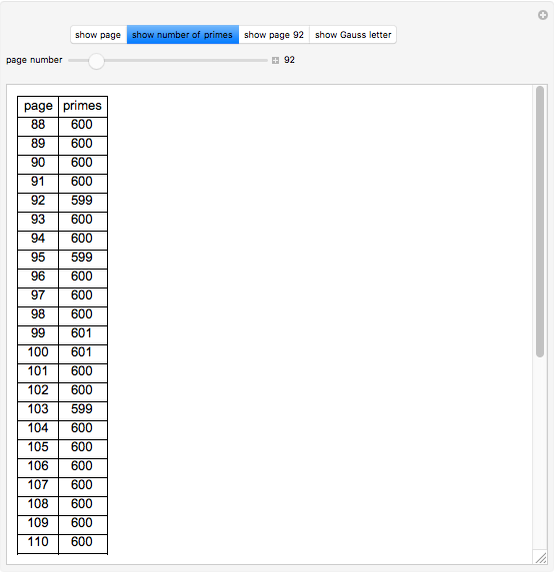
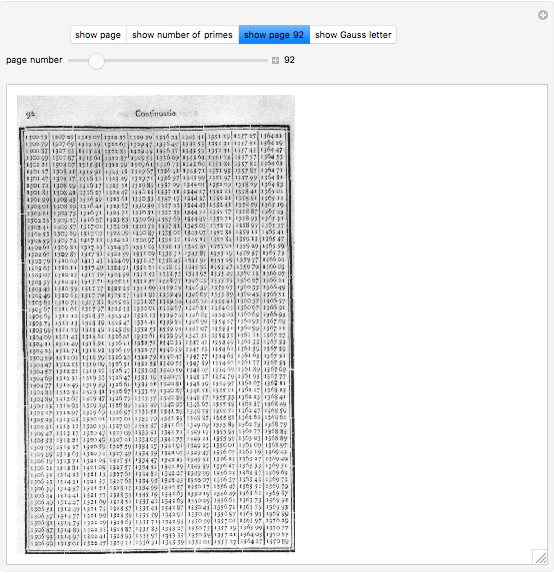
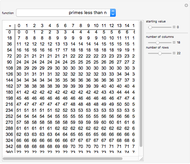
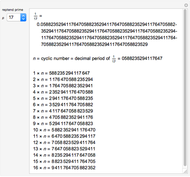
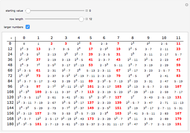
In 1797 Vega published a table of prime numbers from 102001 to 400031. On each of the pages 88–127 there are 600 numbers in 10 columns with 60 numbers. Page 128 has 6 columns with 16 numbers. While there are no mistakes on this page, there are on some other pages. This reconstruction corrects some of the mistakes.

[more]

Contributed by: Izidor Hafner (August 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

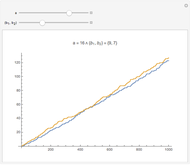
Based on the tables by Anton Felkel and Jurij Vega, Adrien-Marie Legendre conjectured in 1797 or 1798 that 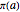is approximated by the function 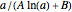, where and 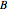are unspecified constants [1].

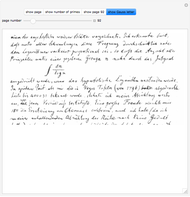
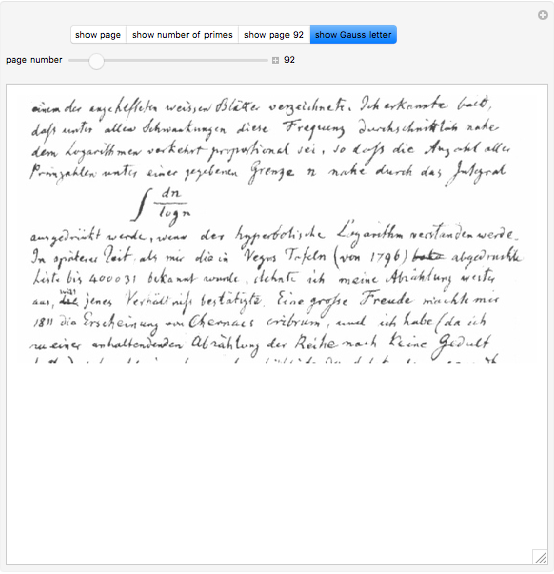
Carl Friedrich Gauss considered the same question as we see from a letter to Encke (1849), where Vega's tables were mentioned.

Vega's 1797 table of primes was based on Felkel's table [2].

References

[1] Wikipedia. "Prime Number Theorem." (Aug 18, 2013) en.wikipedia.org/wiki/Prime_number_theorem # Approximations_for _the _nth _prime _number.

[2] D. Roegel. "A Reconstruction of Vega's Table of Primes and Factors." (October 9, 2011) locomat.loria.fr/vega1797/vega1797doc.pdf.

[3] G. Vega, Logarithmische, trigonometrische, und andere zum Gebrauche der Mathematik eingerichtete Tafeln und Formeln, Leipzig: Weidmannischen Buchhandlung, 1797. www.dlib.si/details/URN:NBN:SI:DOC-OY967PMX/?browse=knjige&node=besedila%2f3&pageSize=25&query=%27source%3dknjige%40AND%40UDC%3dMatematika%40AND%40keywords%3dvega%27.

Permanent Citation

Izidor Hafner "Reconstruction of Vega's Prime Number Table"
http://demonstrations.wolfram.com/ReconstructionOfVegasPrimeNumberTable/
Wolfram Demonstrations Project
Published: August 21 2013


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send

Reconstruction of Vega's Prime Number Table

Snapshots

Details

Related Links

Permanent Citation