Reflected and Transmitted Newton's Rings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
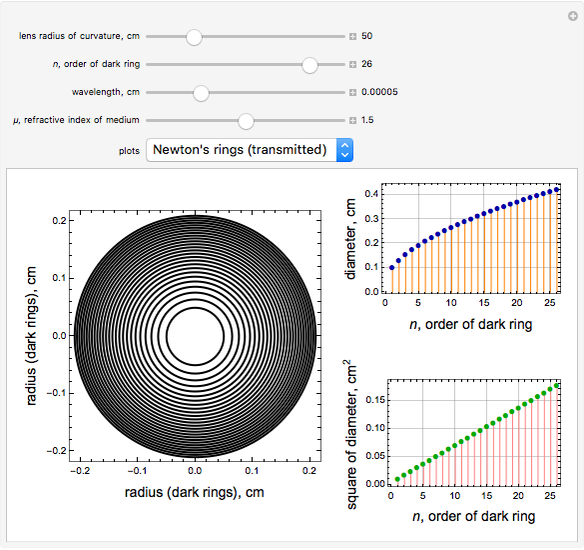
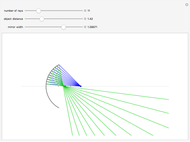
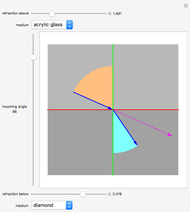
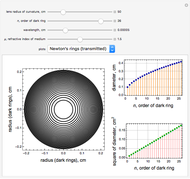
Newton's rings had been earlier observed by Robert Boyle and Robert Hooke, but the first experimental measurement of their radii was done by Isaac Newton. The theoretical explanation given by Thomas Young gives the relation between the wavelength of light 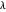 , the radius of curvature
, the radius of curvature 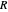 of a given plano-convex lens, the squares of diameters
of a given plano-convex lens, the squares of diameters 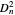 of the circular interference rings, the refractive index
of the circular interference rings, the refractive index  of the region where the rings are formed and
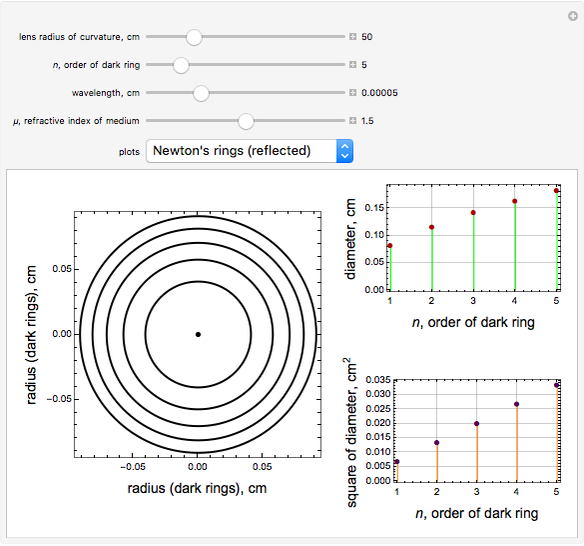
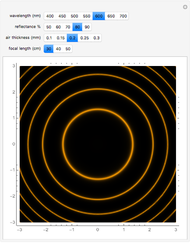
of the region where the rings are formed and 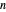 , the order of the ring. For Newton's rings formed from reflected light, the center ring is dark and the diameters of the dark and bright rings are given by
, the order of the ring. For Newton's rings formed from reflected light, the center ring is dark and the diameters of the dark and bright rings are given by 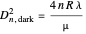 and
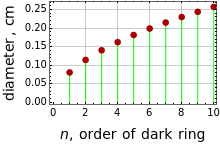
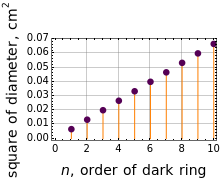
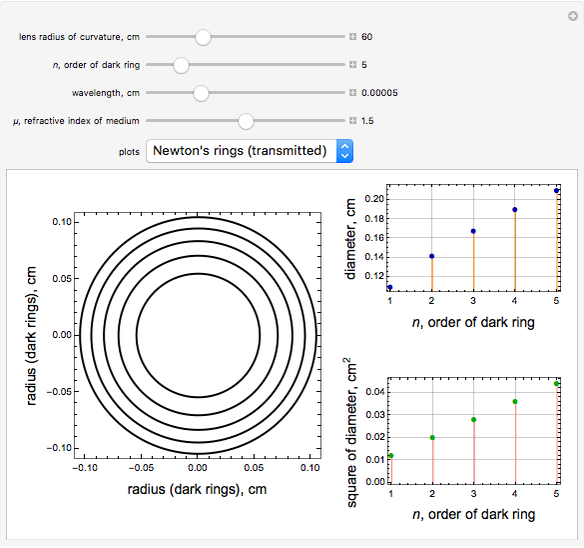
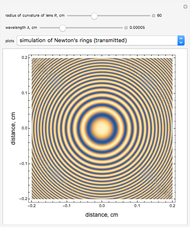
and 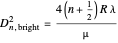 . For Newton's rings formed from transmitted light, the reverse is true. The center ring is bright and the relations for the diameters of the dark and bright rings are now
. For Newton's rings formed from transmitted light, the reverse is true. The center ring is bright and the relations for the diameters of the dark and bright rings are now 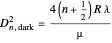 and
and 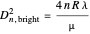 .
.
Contributed by: Kallol Das (December 2017)
Dept. of Physics, St. Aloysius' College (Autonomous), Jabalpur, India
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] A. N. Matveev, Optics, Moscow: Mir Publishers, 1988.
[2] F. A. Jenkins and H. E. White, Fundamentals of Optics, 3rd. ed., New York: McGraw-Hill, 1957.
Permanent Citation