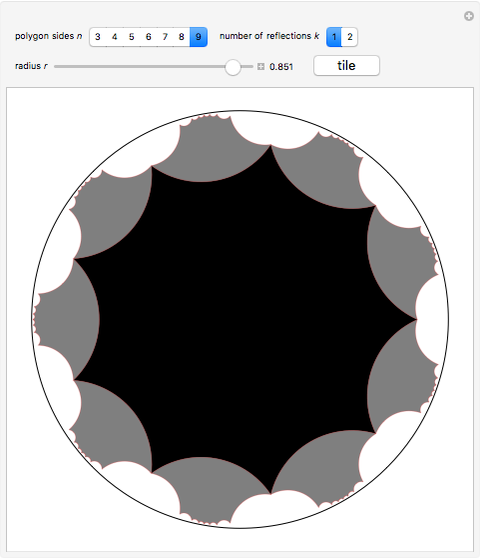
Reflecting a Regular Polygon across Its Sides in the Hyperbolic Plane
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In the hyperbolic plane, given 
and 
, there is a unique positive real number 
such that the regular -gon 
of side length tiles the whole plane, with copies of touching at each vertex. This Demonstration shows how the tiling fails when the side length differs from .
Contributed by: Gasper Zadnik (April 2013)
Suggested by: George Beck
Open content licensed under CC BY-NC-SA
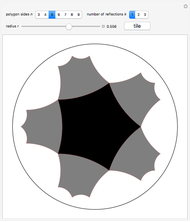
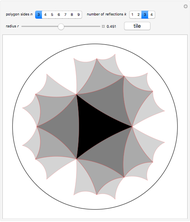
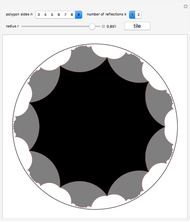
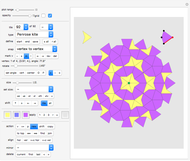
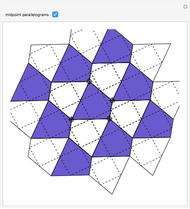
Snapshots
Details
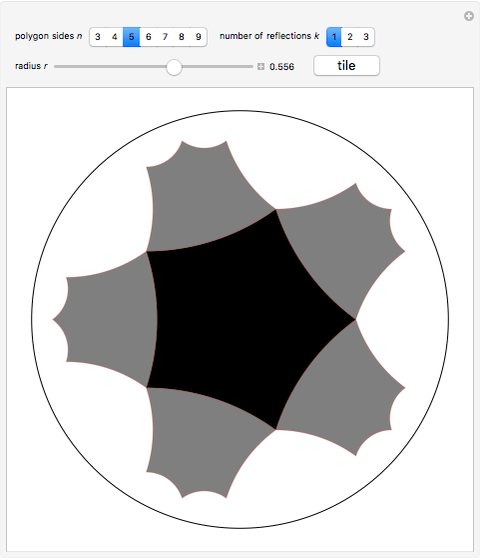
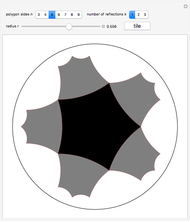
Select the number of sides of and choose its side length via the Euclidean radius 
of its circumscribed circle. Also select the number of stages you want to see; by default, you see only the central tile and its reflections over its sides. By increasing the number of stages 
, you can also see the reflections of reflections (and so on) of the central tile over its sides.
The button "tile" calculates such that the graphic is indeed the tiling. Other values cause the reflections to have gaps or to overlap.
Permanent Citation
Tiling the Hyperbolic Plane with Regular Polygons
Ga?per Zadnik
Chains of Regular Polygons and Polyhedra
George Beck
The Disappearing Hyperbolic Squares
Stan Wagon
Poincaré Hyperbolic Disk
Eric W. Weisstein
Hyperbolic Quadrilateral
Ron Grosz
Hyperbolic Triangle
Michael Rach and Ron Grosz
Tiling Constructor
Karl Scherer
Multiple Reflections of a Regular Polygon in Its Sides
George Beck
Iteratively Reflecting a Point in the Sides of a Triangle
George Beck
Any Quadrilateral Can Tile
George Beck
