Reflection of Parallel Rays by a Two-Dimensional Body of Nearly Maximal Resistance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration shows a class of nonconvex bodies that maximize resistance as they move forward while slowly rotating through a rarefied medium. This class of shapes yields a resistance very close to the theoretical maximum, improving all previous results found by the authors.
Contributed by: Paulo D. F. Gouveia (March 2011)
After work by: Paulo D. F. Gouveia, Alexander Plakhov, and Delfim F. M. Torres
Open content licensed under CC BY-NC-SA
Snapshots
Details
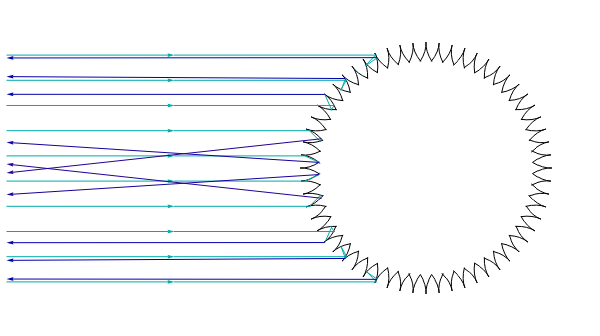
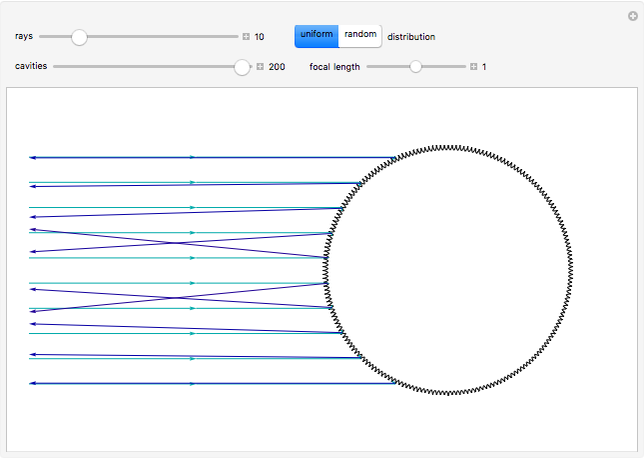
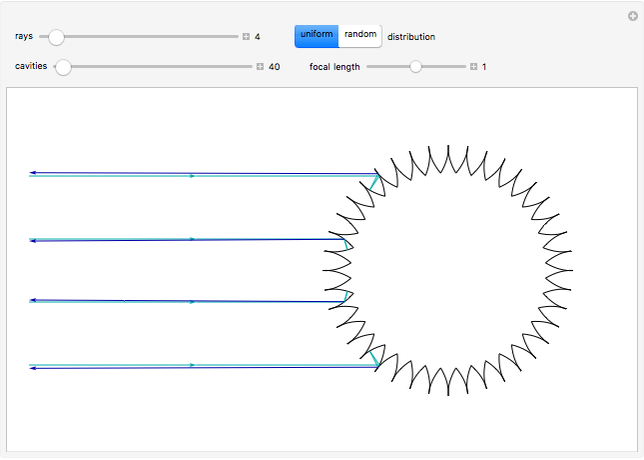
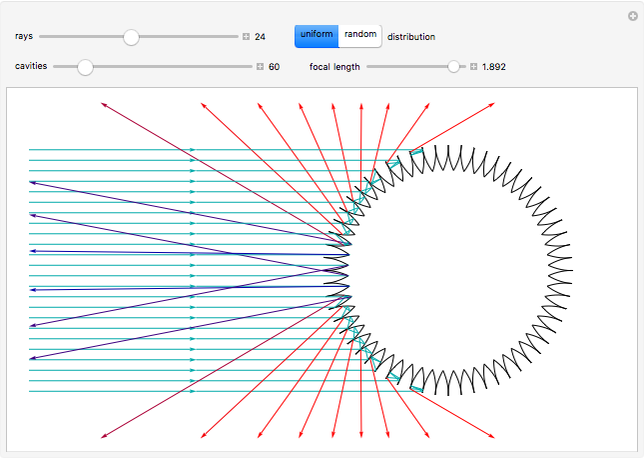
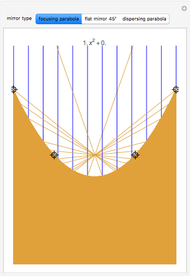
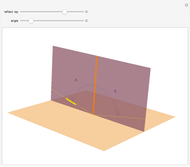
A two-dimensional body, exhibiting a slight rotational movement, moves in a rarefied medium of particles that collide with it in a perfectly elastic way. In [1], shapes of nonconvex bodies were sought that would maximize the braking force of the medium on their movement. Further results presented in [2] and illustrated here show a two-dimensional shape that is very close to its theoretical supremum value.
The contour of this body has cavities with a shape formed by two equal arcs of symmetrical parabolas, where the focus of each one coincides with the vertex of the other (so that the focal length is 1). This Demonstration shows the reflection of parallel rays by this body. It is possible to verify that the rays are reflected at a velocity that is nearly opposite to the entry velocity, which characterizes a body of maximal resistance.
References: [1] A. Yu. Plakhov and P. D. F. Gouveia, "Problems of Maximal Mean Resistance on the Plane." Nonlinearity, 20, 2007 pp. 2271–2287. [2] P. D. F. Gouveia, A. Plakhov, and D F. M. Torres, "Two-Dimensional Body of Maximum Mean Resistance," Applied Mathematics and Computation, 215, 2009 pp. 37–52.