Relaxation of a Discrete Maxwell Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
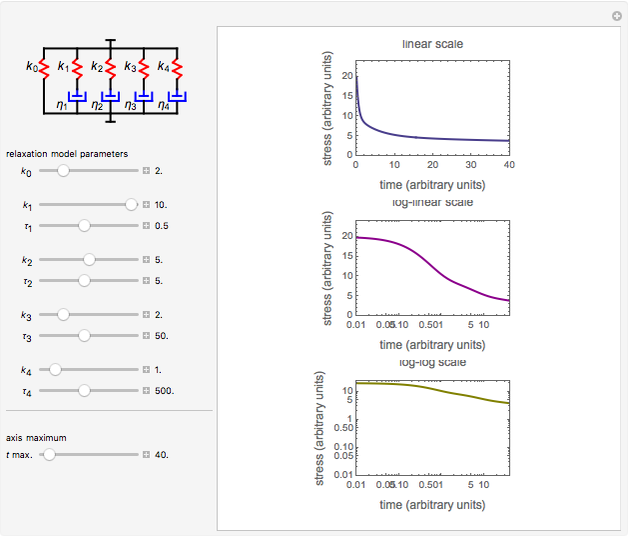
The discrete Maxwell model has been used extensively in the rheological characterization of foods and agricultural products subjected to uniaxial deformation. This Demonstration shows how properties and relative weights of the model elements affect the relaxation curve’s shape in linear, log-linear, and log-log plots. It also shows how elements with short and long relaxation times affect the same curve’s shape when viewed on different time scales.
Contributed by: Mark D. Normand and Micha Peleg (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
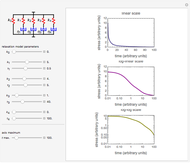
Snapshot 1: liquid dominated by short relaxation times
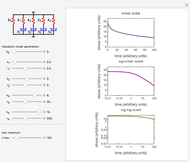
Snapshot 2: liquid dominated by long relaxation times
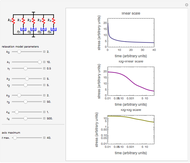
Snapshot 3: solid dominated by short relaxation times
Snapshot 4: solid dominated by long relaxation times
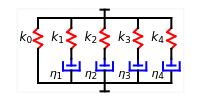
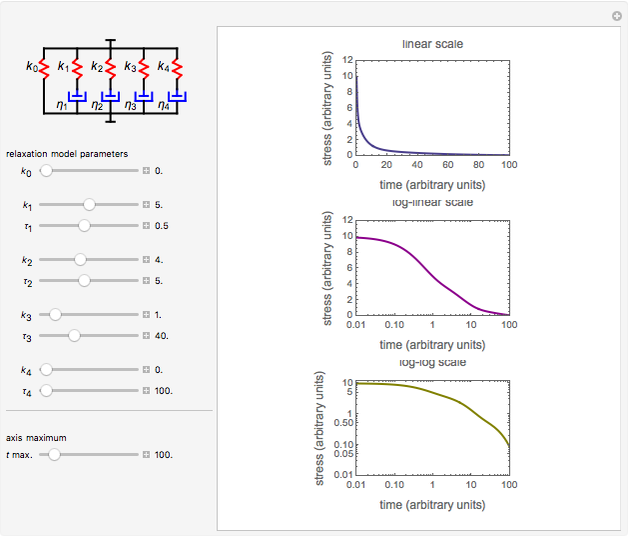
This Demonstration generates stress relaxation curves produced by a discrete Maxwell model having a spring in parallel to four Maxwell elements with increasing relaxation times subjected to a unit strain. The model’s relaxation equation is 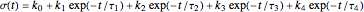 , where the
, where the 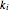 are the elements' elastic components’ (springs’ moduli) and the
are the elements' elastic components’ (springs’ moduli) and the 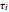 their relaxation times,
their relaxation times, 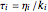 . The free spring is equivalent to a Maxwell element with
. The free spring is equivalent to a Maxwell element with 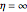 . According to this model,
. According to this model, 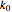 is positive for a viscoelastic solid and zero for a liquid.
is positive for a viscoelastic solid and zero for a liquid.
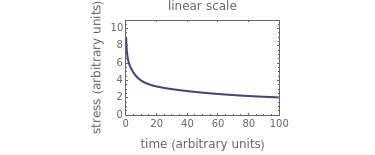
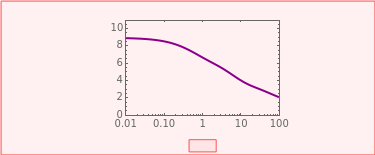
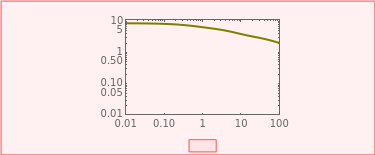
Use sliders to enter the elements’ parameter values and the experiment’s duration,  . The corresponding relaxation curve is drawn on linear coordinates (top), linear-logarithmic coordinates (center), and as a log-log plot (bottom).
. The corresponding relaxation curve is drawn on linear coordinates (top), linear-logarithmic coordinates (center), and as a log-log plot (bottom).
References
[1] D. R. Bland, The Theory of Linear Viscoelasticity, New York: Pergamon Press, 1960.
[2] W. N. Findley, J. S. Lai, and K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, New York: North–Holland Publishing Company, 1976.
Permanent Citation