Repeatedly Subdividing Triangles through Special Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
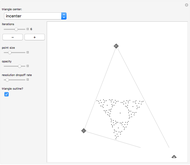
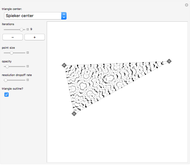
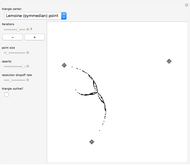
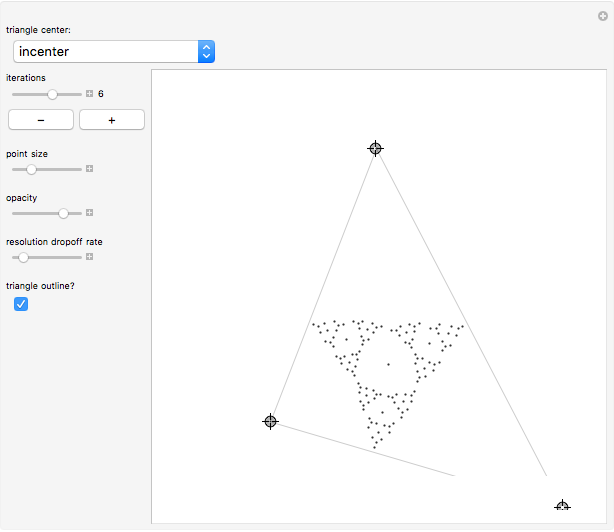
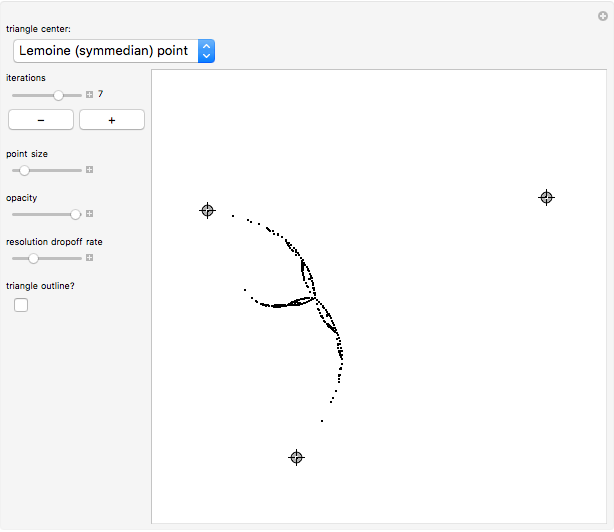
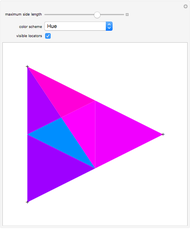
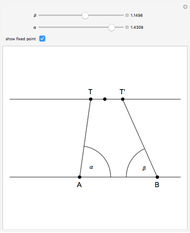
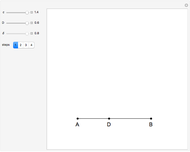
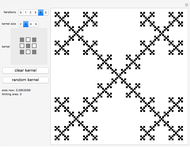
Associated with every triangle are a number of special points called "triangle centers". Some of the best known of these include the centroid, incenter, and circumcenter; many more have been named and studied. Not all triangle centers, in fact, fall in the interior of a given triangle, but some always do. We can draw segments from the vertices to one of these interior triangle centers to subdivide the triangle into three new ones. Iterating this process can produce some beautiful figures. This Demonstration shows the centers of all the subtriangles up to the 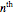 iteration.
iteration.
Contributed by: Ethan Beihl (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Demonstration displays fewer points from each triangle for later iterations. To sample more points, move the "resolution dropoff rate" slider to the left. The number of points is chosen according to the formula  , where
, where  is the total number of iterations,
is the total number of iterations, 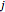 is the current iteration, and
is the current iteration, and  is the dropoff rate selected on the slider.
is the dropoff rate selected on the slider.
The process of subdividing a polygon into smaller triangles is called triangulation. It is very important in geometry and topology and is of enormous relevance to computer graphics algorithms, where it is used for the refinement of polygonal meshes.
More information on the various triangle centers that have distinguished themselves over the years is available at Kimberling's monumental Encyclopedia of Triangle Centers.
References
[1] S. Butler and R. Graham, "Iterated Triangle Partitions," Fete of Combinatorics and Computer Science, Bolyai Society Mathematical Studies 20, 2010 pp. 23–42. PDF available online at http://orion.math.iastate.edu/butler/papers/iterated_triangles.pdf.
[2] C. Kimberling, Encyclopedia of Triangle Centers [online]. (Jul 4, 2015) faculty.evansville.edu/ck6/encyclopedia/ETC.html.
Permanent Citation