Replicator-Mutator Dynamics with Three Strategies

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
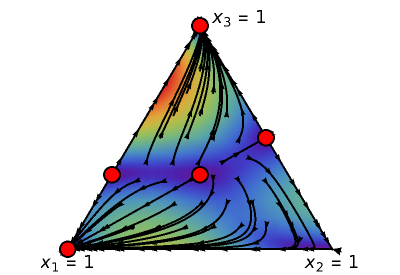
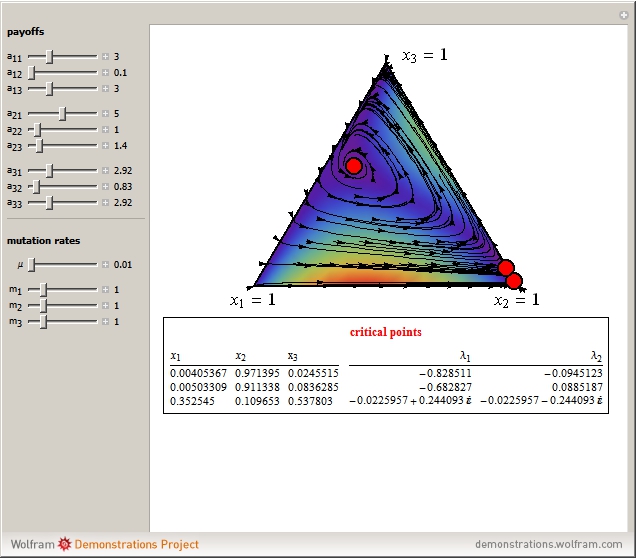
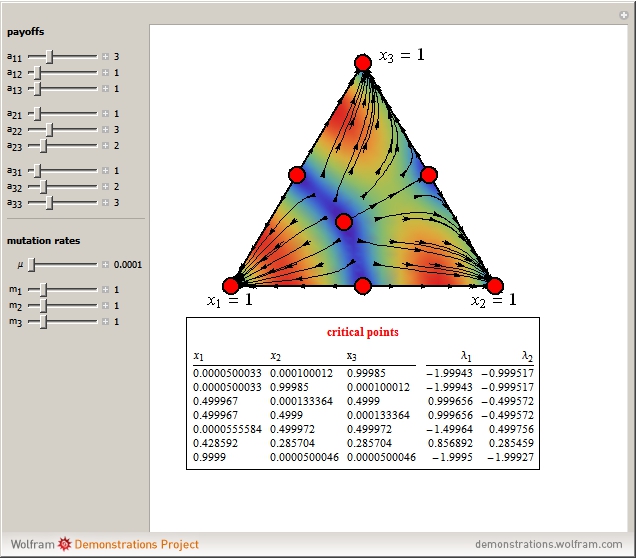
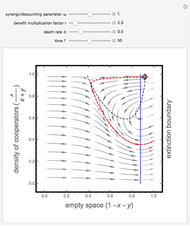
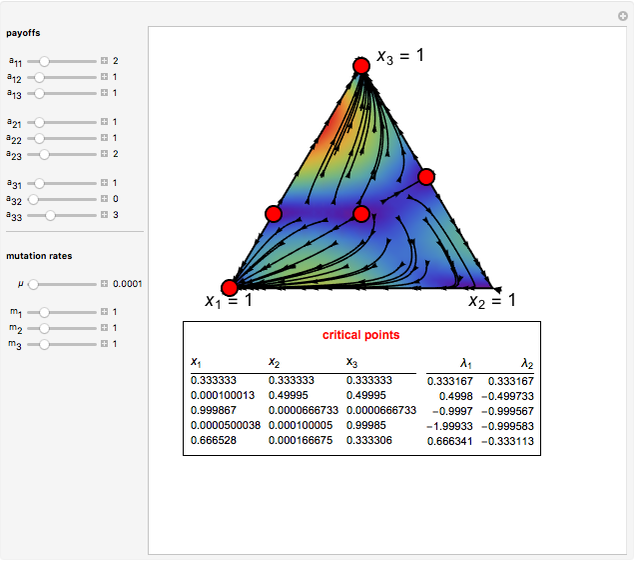
This Demonstration shows the phase portrait in an equilateral triangle of the replicator-mutator dynamics with three strategies. The parameters  denote the payoff that an
denote the payoff that an 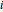 -strategist obtains in an interaction with a
-strategist obtains in an interaction with a  -strategist. The parameter
-strategist. The parameter  denotes the total fraction of mutants or entrants in the population. The parameters
denotes the total fraction of mutants or entrants in the population. The parameters  denote the weights given by mutants to strategy
denote the weights given by mutants to strategy 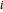 , so
, so 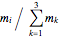 is the fraction of mutants that adopt strategy
is the fraction of mutants that adopt strategy 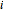 . This Demonstration also calculates the critical points of the system and their corresponding eigenvalues, which are helpful in assessing the dynamic stability of the critical point.
. This Demonstration also calculates the critical points of the system and their corresponding eigenvalues, which are helpful in assessing the dynamic stability of the critical point.
Contributed by: Luis R. Izquierdo and Segismundo S. Izquierdo (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
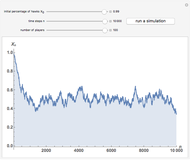
Snapshot 1: system analyzed in [1]
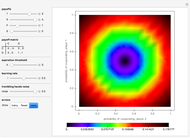
Snapshot 2: if the payoff matrix is symmetric (which corresponds to the standard population-genetic model of natural selection on a large diploid population), a global Lyapunov function can be found that excludes cyclic behavior and guarantees that all orbits converge to the set of fixed points; see [2]
Snapshot 3: rock-scissors-paper game
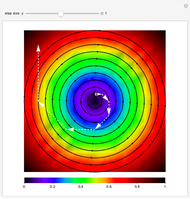
Snapshot 4: strictly dominated strategies in the replicator-mutator dynamics can have an influence on the location of the limit rest points for small mutation; see [3]
References
[1] L. A. Imhof, D. Fudenberg, and M. A. Nowak, "Evolutionary Cycles of Cooperation and Deflection," in Proceedings of the National Academy of Sciences, 102(31), 2005 pp. 10797–10800. http://www.pnas.org/content/102/31/10797.
[2] J. Hofbauer, "The Selection Mutation Equation," Journal of Mathematical Biology, 23, 1985 pp. 41–53, http://dx.doi.org/10.1007/BF00276557.
[3] S. S. Izquierdo and L. R. Izquierdo, "Strictly Dominated Strategies in the Replicator-Mutator Dynamics," Games 2(3), 2011 pp. 355–364, http://dx.doi.org/10.3390/g2030355.
Permanent Citation
"Replicator-Mutator Dynamics with Three Strategies"
http://demonstrations.wolfram.com/ReplicatorMutatorDynamicsWithThreeStrategies/
Wolfram Demonstrations Project
Published: July 1 2011