Residual-Fit Spread Plot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
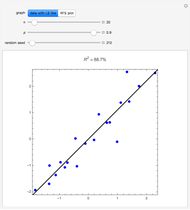
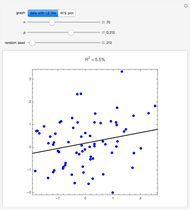
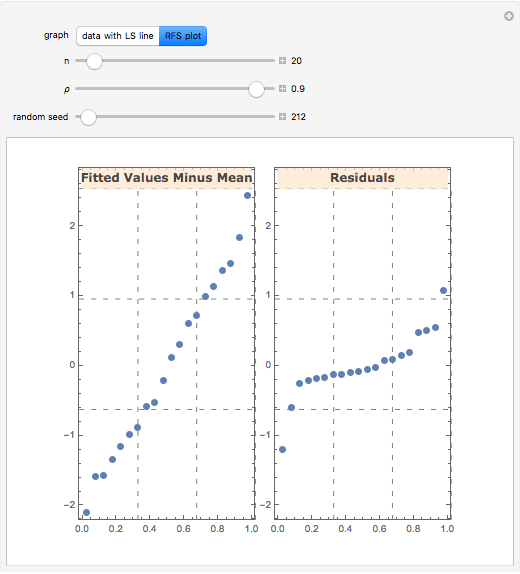
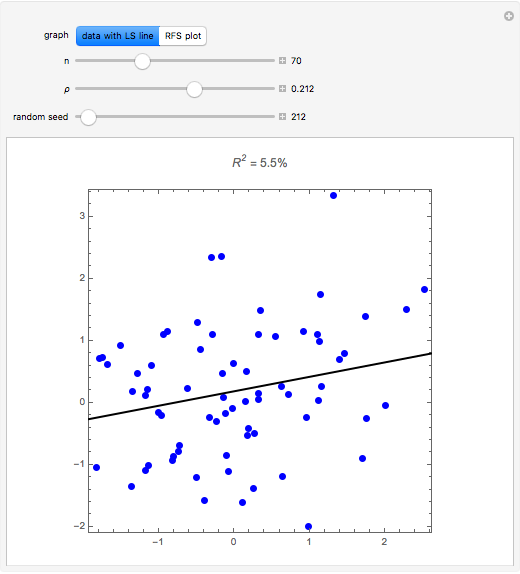
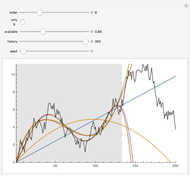
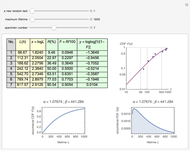
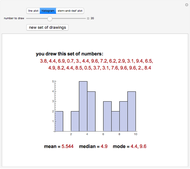
The residual-fit spread (RFS) plot is illustrated using simple linear regression. In general, the purpose of the RFS plot is to provide a visualization of how well a statistical model fits the data. It provides a graphical alternative to the coefficient of determination.
[more]
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
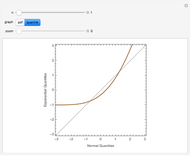
The RFS plot and trellis-style graphics were introduced in [1] and [2]. The plot is a two-panel display of the quantile plot of the fitted values minus their mean, and of the residuals. The quantile plot for data 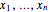 is the plot of
is the plot of  versus
versus 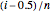 , where
, where  are other ordered values,
are other ordered values, 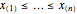 . Many examples of the use of the quantile plot are discussed in [2] where its advantages over the histogram for data visualization are discussed.
. Many examples of the use of the quantile plot are discussed in [2] where its advantages over the histogram for data visualization are discussed.
[1] R. A. Becker, W. S. Cleveland, and M. Shyu, "The Visual Design and Control of Trellis Display," Journal of Computational and Graphical Statistics, 5(2), 1996 pp. 123–155.
[2] W. S. Cleveland, Visualizing Data, Summit, NJ: Hobart Press, 1993.
Permanent Citation