Residue Curve Map for a Non-Ideal Ternary Mixture with a Distillation Boundary

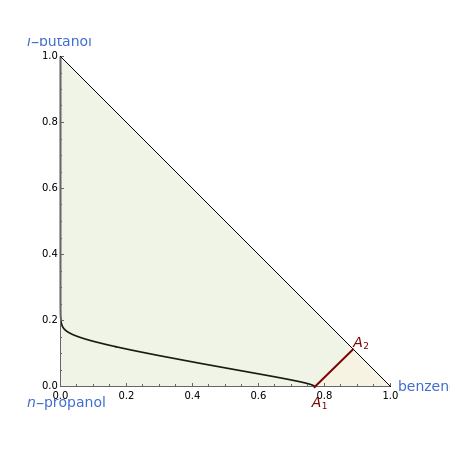
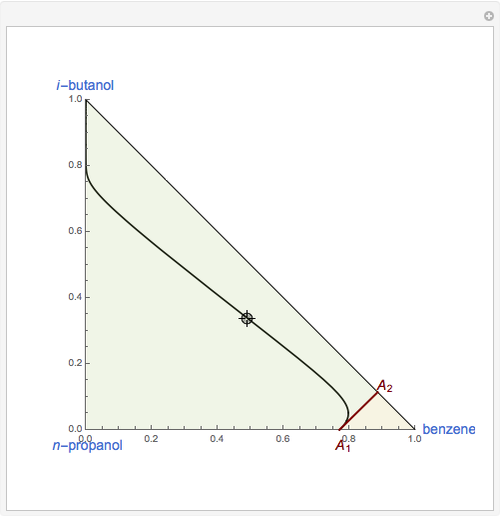
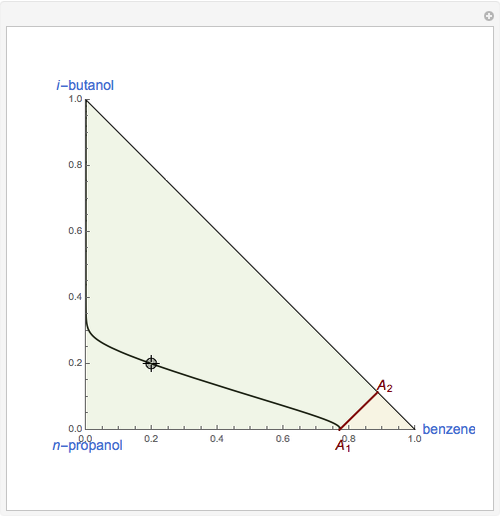
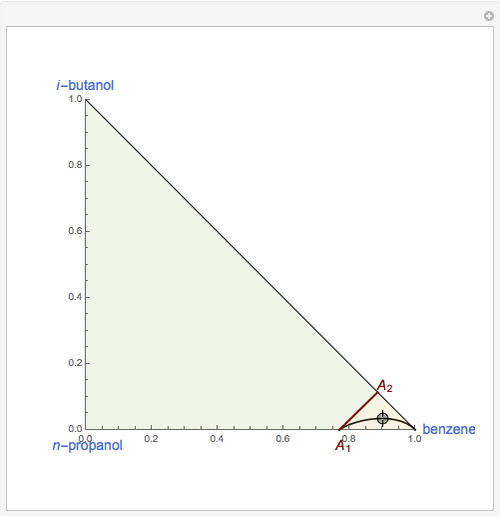
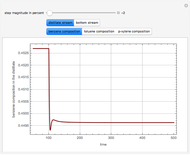
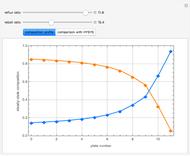
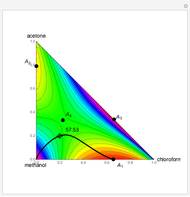
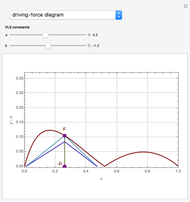
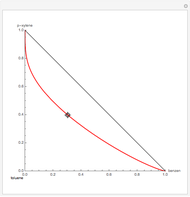
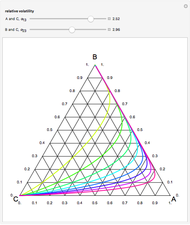
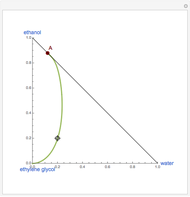
This Demonstration plots the residue curve of a non-ideal ternary mixture composed of benzene, -butanol and -propanol. Deviation from ideal behavior in the liquid phase is taken into account using the Wilson model in order to compute the activity coefficients. The total pressure is 101.325 kPa. This mixture presents two azeotropes: (1) between benzene and -propanol, marked in the ternary diagram by 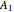(77% mole fraction of benzene); (2) between benzene and 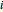-butanol, marked in the ternary diagram by 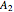(88.62% mole fraction of benzene). This ternary mixture has two distillation regions (the yellow and green shaded areas) with a distillation boundary connecting the two binary azeotropes (the straight red segment in the diagram). Benzene and 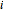-butanol are stable nodes; -propanol and 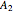are two saddle points, and finally is an unstable node. You can change the position of the locator to plot the residue curve passing at the locator position.