Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Riemann Zeta Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

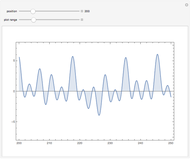
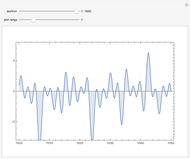
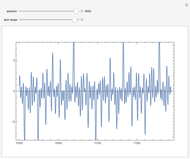
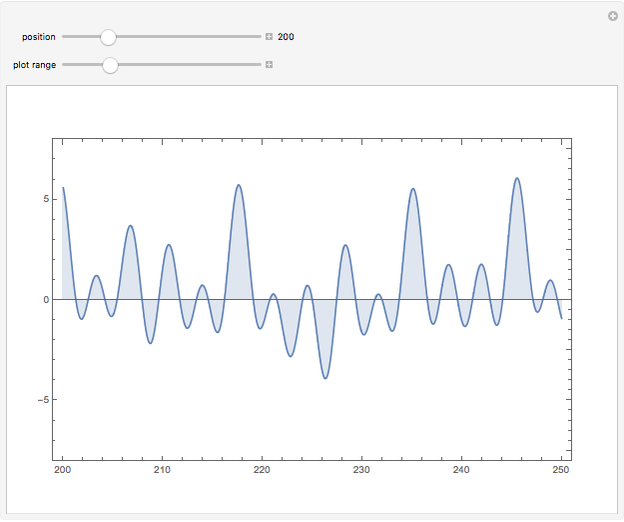
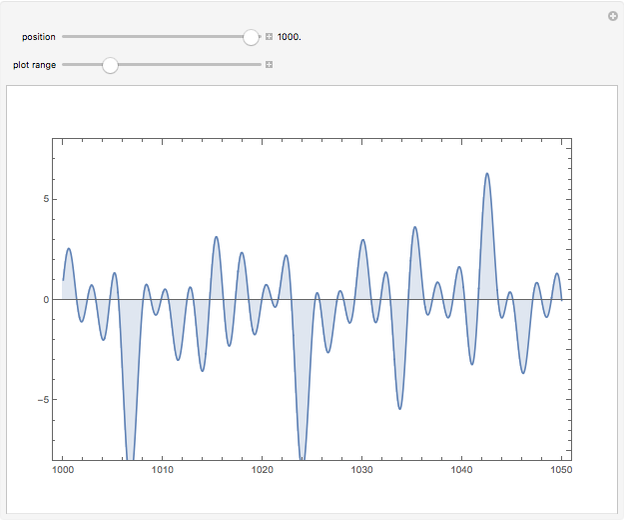
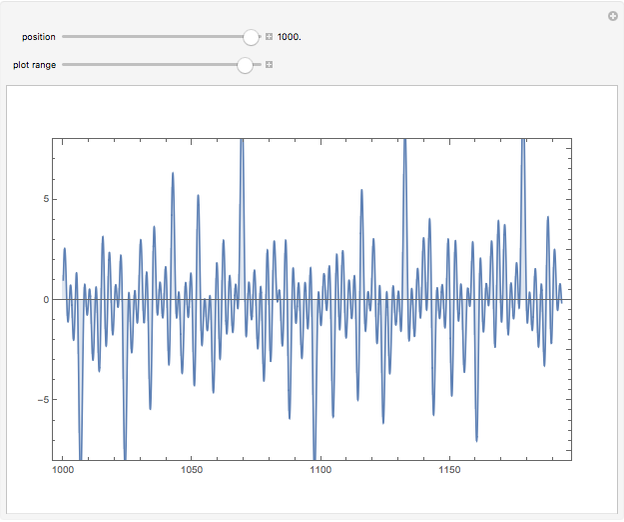
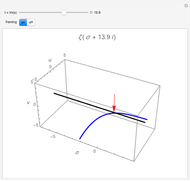
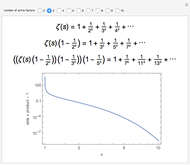
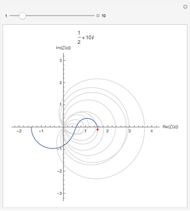
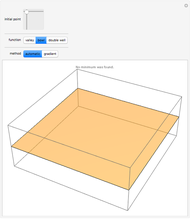
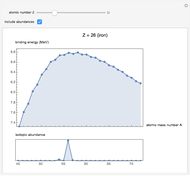
The Riemann zeta function (or, precisely, the Riemann-Siegel Z function) along the critical line. The Riemann hypothesis implies that no minimum should ever lie above the axis.

Contributed by: Stephen Wolfram (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send