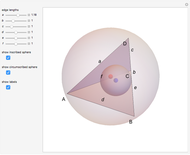
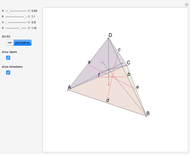
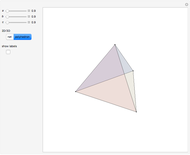
Right-Angled Tetrahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Let 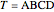 be a tetrahedron with the three plane angles at
be a tetrahedron with the three plane angles at 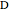 all right angles, that is,
all right angles, that is, 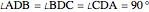 . (This is more explicitly known as a trirectangular tetrahedron.) Let
. (This is more explicitly known as a trirectangular tetrahedron.) Let  ,
, 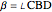 ,
, 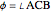 . Then
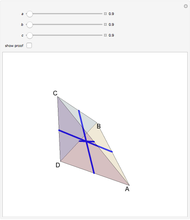
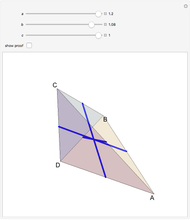
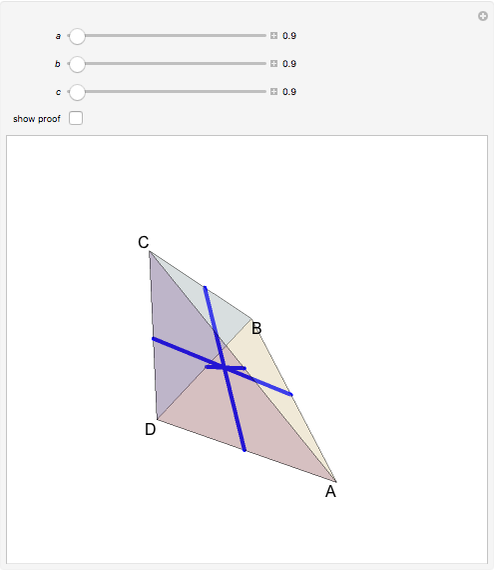
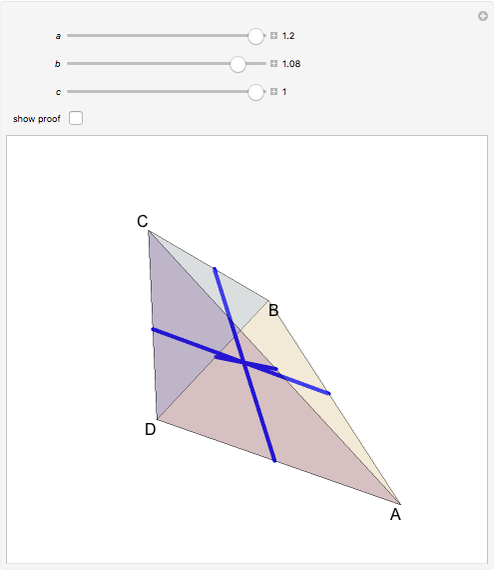
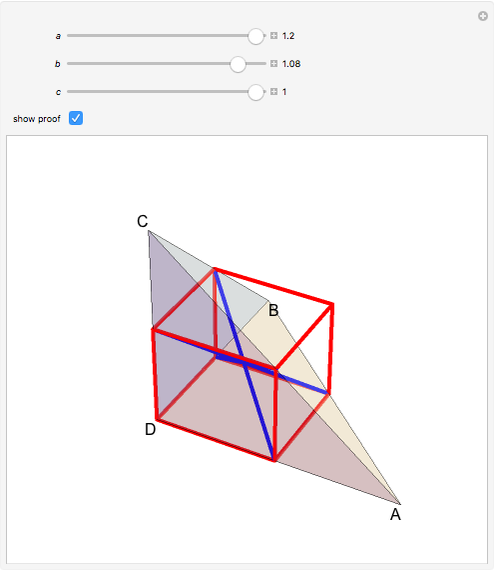
. Then 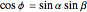 . The lines that join the midpoints of opposite edges are equal and meet at a point. The proof, outlined in the Details, implies that these three lines are diagonals of a rectangular prism, intersecting at the center.
. The lines that join the midpoints of opposite edges are equal and meet at a point. The proof, outlined in the Details, implies that these three lines are diagonals of a rectangular prism, intersecting at the center.
Contributed by: Izidor Hafner (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Proof
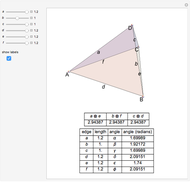
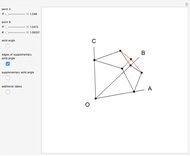
Let  . Then
. Then 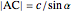 ,
,  ,
, 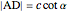 ,
, 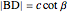 . The length of
. The length of 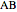 can be evaluated from triangle
can be evaluated from triangle 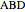 using the Pythagorean theorem,
using the Pythagorean theorem, 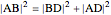 , and from triangle
, and from triangle 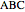 using the law of cosines,
using the law of cosines, 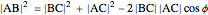 , giving
, giving
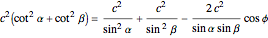 .
.
Simplifying this identity, we find: 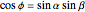 [1, pp. 102 and 117].
[1, pp. 102 and 117].
Reference
[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.
Permanent Citation