Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

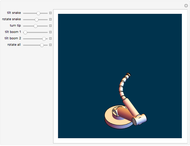
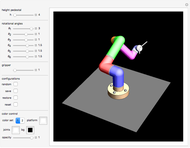
Robotics Application of Lissajous Curves

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

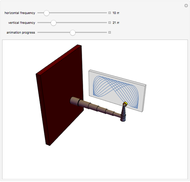
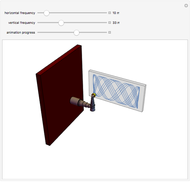
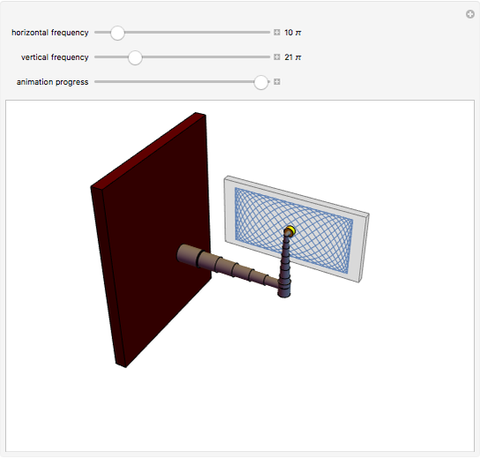
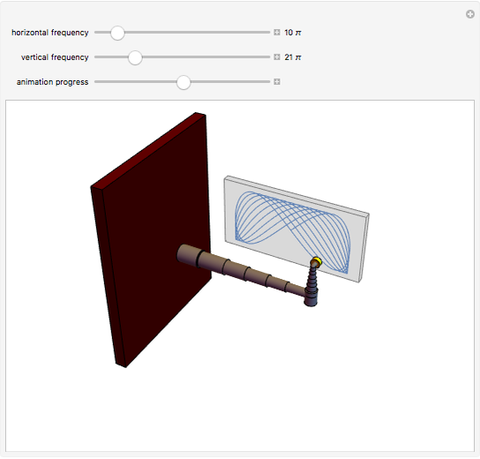
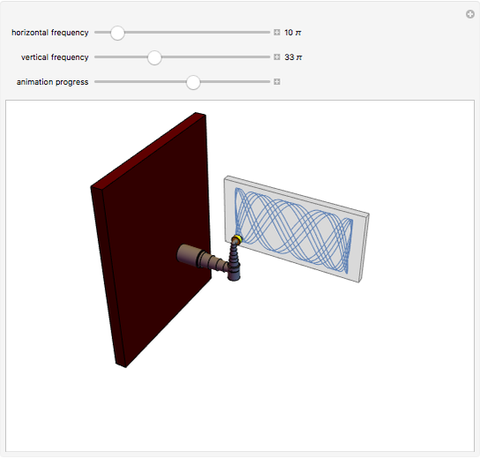
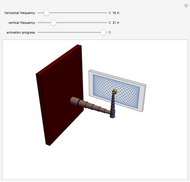
This Demonstration shows a polishing robotic arm whose pad moves following a Lissajous curve, which is being drawn in the screen during the animation. You can vary the frequencies of the vertical and horizontal movements using their respective controls. According to these values, different curves are constructed. The animation finishes when the curve has completed a whole period. The animation simulates the movement of the individual parts that form the robotic arm.

Contributed by: Francisco Velázquez (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The movement is determined by the parametric function (horizontal movement) and (vertical movement), where and are the frequencies for each function. Since these frequencies are multiples of , the period of the Lissajous curve is calculated as the least common multiple (LCM) of the vertical and horizontal periods; the animation finishes when the period of the curve is completed. If you change the frequencies, the period will be recalculated instantly. The animation progress control does not depend on the period of the curve.

Based on an exercise taken from [1].

Reference

[1] H. Anton, I. Bivens, and S. Davis, Calculus—Early Transcendentals, 9th ed., New York: John Wiley & Sons, 2008.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send