Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

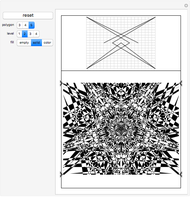
Root-Finding Fractals

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

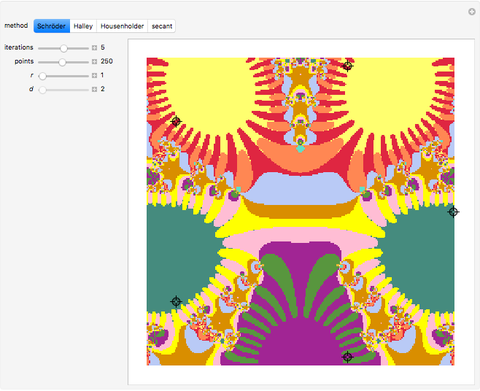
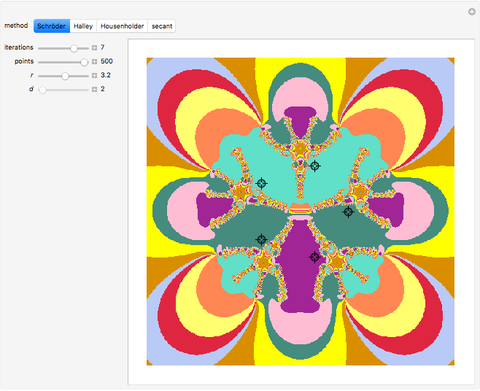
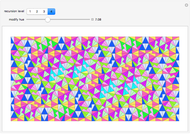
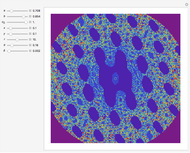
This Demonstration shows fractals created with different iterative root-finding methods in a region of radius in the complex plane. The number of locators specifies the degree of the polynomial being approximated and their positions are the values of the roots. The parameter in the Housenholder method defines the order of the derivatives.

Contributed by: Enrique Zeleny (December 2014)
Based on a program by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA

Snapshots

Details

Here are the different methods and the expressions used to approximate roots (starting with an initial guess ).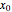

Schröder:

.

Halley:

.

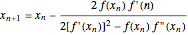Housenholder:

.

Secant:

.

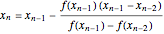Reference

[1] "Root-Finding Fractals," Softology's Blog. (Dec 16, 2014) softologyblog.wordpress.com/2011/01/20/root-finding-fractals.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send