Rotating Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
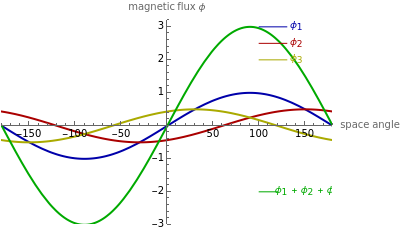
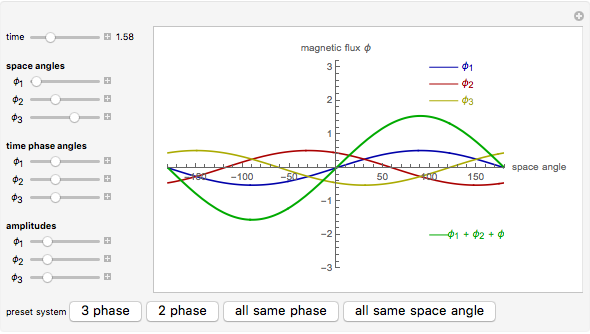
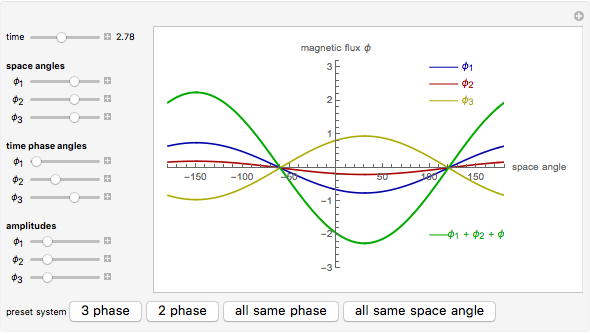
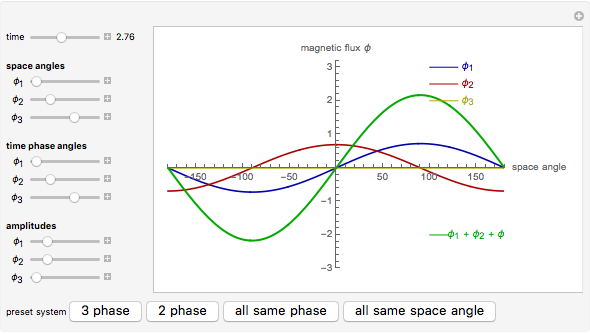
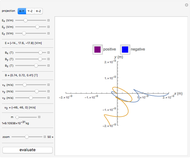
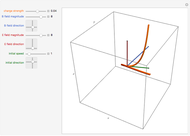
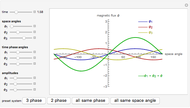
This Demonstration shows how combining two or three magnetic fluxes varying in space and time can be used to generate a rotating magnetic field inside an electrical device. The horizontal axis gives the angle in degrees measured from a fixed axis and the vertical axis gives the magnitude of the flux. So at a given time, the graphs for 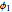 ,
, 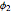 , and
, and  give the variation of these fluxes with the angle. The green curve gives the resultant sum of the fluxes.
give the variation of these fluxes with the angle. The green curve gives the resultant sum of the fluxes.
Contributed by: Rajendra Adhikari (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The fluxes vary as 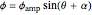 , where
, where  is the angle from the fixed axis,
is the angle from the fixed axis,  is the angle of the orientation of the coil creating that flux (or the angle for peak flux), and
is the angle of the orientation of the coil creating that flux (or the angle for peak flux), and 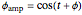 is the time varying amplitude of the flux, with phase shift of
is the time varying amplitude of the flux, with phase shift of  . By changing the slider for space angle, you can change the orientation of the coils in space so that the maximum flux is produced at different angles. Hence, the peaks of the graph for
. By changing the slider for space angle, you can change the orientation of the coils in space so that the maximum flux is produced at different angles. Hence, the peaks of the graph for 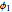 ,
, 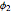 , and
, and  represent the orientation of the coils and hence are fixed. Only the amplitudes of
represent the orientation of the coils and hence are fixed. Only the amplitudes of 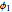 ,
, 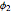 , and
, and  change with time. The controls for the time phase angles specify what time delay is needed for that particular flux to reach its maximum. Only through intelligent choices of the space angles and time delay angles is it possible to combine those fluxes to create a rotating magnetic field. But, not to worry, presets are available.
change with time. The controls for the time phase angles specify what time delay is needed for that particular flux to reach its maximum. Only through intelligent choices of the space angles and time delay angles is it possible to combine those fluxes to create a rotating magnetic field. But, not to worry, presets are available.
Permanent Citation