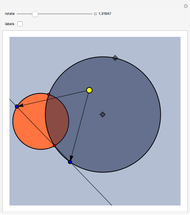
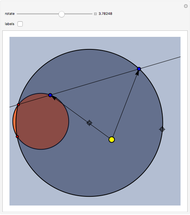
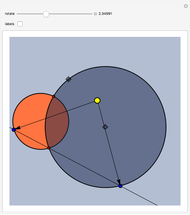
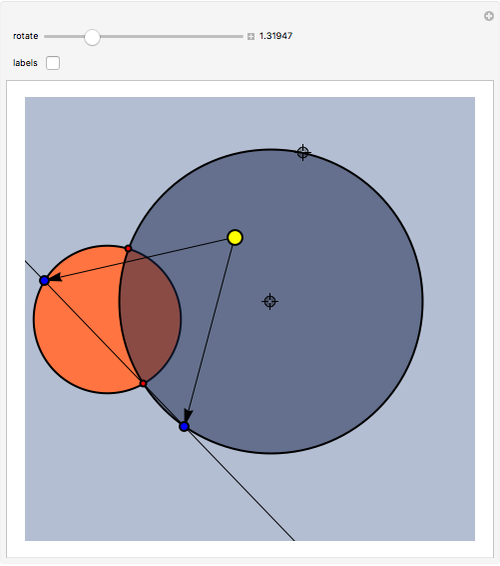
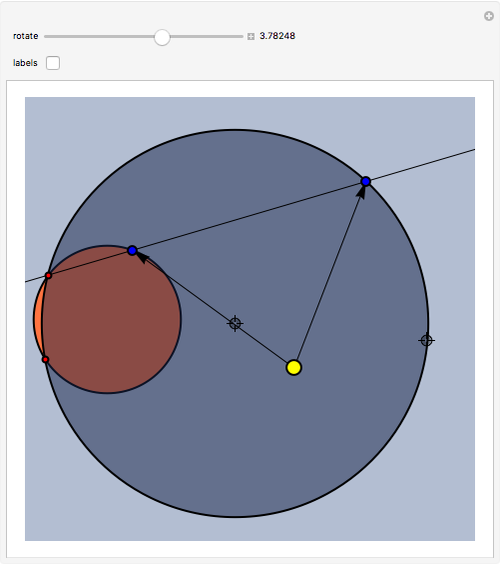
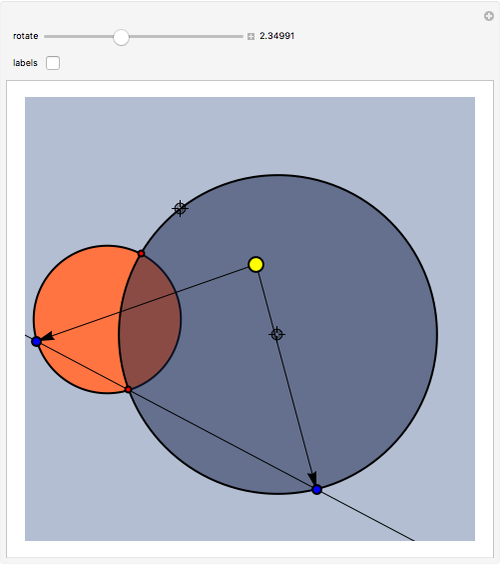
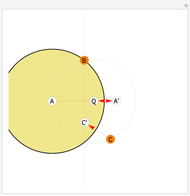
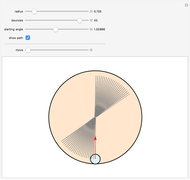
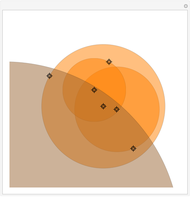
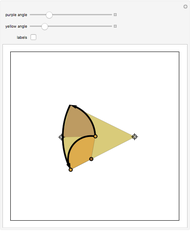
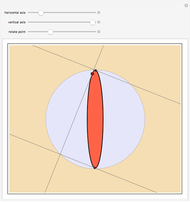
This Demonstration illustrates a problem from the Australian Mathematical Olympiad held in 1979. Consider two intersecting circles—in our implementation the orange circle is fixed and there are two locators to modify the blue circle. Let and 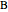be the two red points of intersection. Starting simultaneously from , two (blue) points and move with constant speeds around the two circles in the same direction. The two points return to simultaneously after one revolution. Then 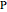, , 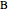and are always collinear and there is a fixed point (the yellow disk) such that, at any time, the distances from 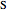to the moving points are equal.